Following up on my post explaining Monomials and Polynomials, here I would like to provide a bit more of an explanation about how to actually work with these terms. In particular, first I am going to show you how to multiply a monomial by a polynomial. Then I will similarly show you how to divide a polynomial by a monomial. And then finally, I will explain the very important concept of FOIL for multiplying to binomials. Nothing too difficult, but all key concepts of algebra. Let’s get to it!
How to multiply a Polynomial and a Monomial. It’s actually very easy, probably way easier than it sounds! Let’s step back a bit first, though, and think about how we multiply regular numbers and expressions. Consider the expression (x + y), and say that we want to multiply that by 3. How do we do that? By now, I think this is very straightforward. We first write it out, like this:
(3)(x + y), or 3(x + y)
Next, we multiply each part of the expression (x + y) by 3, and then we can drop the brackets at the end. This is called the Distributive Property, which refers to how we can remove the brackets if we are multiplying (distributing) the one term with all of the terms within the brackets. I don’t think I need to go into more detail than this for this basic operation, but leave me a comment below if you’d like a bit of help with it. Maybe I’ll do a separate post on the Distributive Property. When we’re done, we have this:
3x + 3y
Now let’s extend this method to some more complicated looking terms. Let’s consider multiplying the monomial 5x with the polynomial (3x + 1). I’ll walk through the steps below, and it hopefully will be easy to follow. All we do is abide by the Distributive Property and simply multiply the single term into the brackets with all the other terms.
5x(3x + 1)
5x(3x) + 5x(1)
Now that we have properly distributed the terms, we just have to simplify it and we’re done. The first term becomes 15x2 while the second term becomes simply 5x:
15x2 + 5x
And that is all there is to multiplying a monomial with a polynomial. The key is to follow the Distributive Property and multiply things through where appropriate, and then combine like terms if necessary and simplify!
OK, so now hopefully you followed all that. But what about if we want to go the other way? What if we want to start with a polynomial and then divide by the monomial instead? Again, it’s very similar to operations you are already familiar with. In this case, you might compare it to cancelling and reducing terms. Let’s look at an example and you’ll see what I mean.
Let’s say that we want to divide (8x + 4) by 2. Probably pretty simple, right? We just divide the 2 into all of the terms to reduce them, leaving us with the answer (4x + 1). We can think of this as a big fraction, with the (8x + 4) on the top as the numerator, and the 2 on the bottom as the denominator. Because we are adding the 8x and 4, by the laws of fractions, we can separate everything into two separate fractions with the same denominator: 8x/2 + 4/2. Now, it might be even easier to see how to reduce these to get our final answer.
The same logic applies when we want to divide a polynomial by a monomial. Consider the example of dividing (25x3 + 15x2 – 5x) by 5x. I’ll write it out as a big fraction first (typing these out is not the most obvious way of demonstrating!).
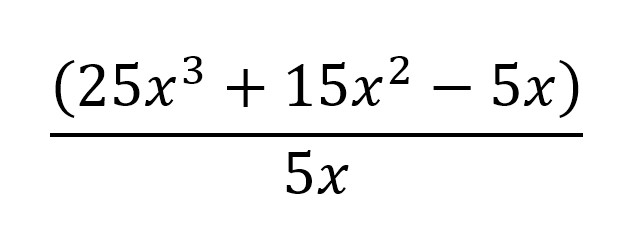
Now, just like with the example above, we can cancel and reduce things. For cancelling, remember that you can only cancel if you are performing the same operation to each term. Or alternately, if you want to split this into the multiple smaller fractions first before simplifying, if that is clearer to you, then that works as well. Either way, you will find that you arrive at the final answer of:
5x2 + 3x – 1
Note that because there is an x term in the denominator, you cancel this out of the numerator for each term by reducing each by x. That is why the powers all reduce by one. The same theory applies to factoring the 5.
Hopefully that explains the two rudimentary concepts of multiplying and dividing monomials and polynomials. Let me know in the comments below if you need any more help!
The last thing I’d like to talk about in this post is FOIL, or how to multiply two binomials. Recall that a binomial is an expression that contains two terms. This is a specific instance of multiplying two polynomials together, though clearly, since polynomials can have many terms, it is best to start simple – so we start here by multiplying two binomials! Larger expressions are not necessarily any harder, though it does become more of a challenge to not mix things up. The key to multiplying any two polynomials is to add up the products of multiplying each term in the first polynomial by each term in the second polynomial.
You have probably heard the expression FOIL when talking about multiplying polynomials, and you will probably see FOIL many times in your studies, so it is best to understand well to what it is referring! FOIL is an acronym that stands for the order of operations that you apply when multiplying two binomials. It only works for binomials, though it still abides by the concept I just outlined for multiplying larger polynomials together. It means FIRST OUTSIDE INSIDE LAST. That probably doesn’t mean much until you see it. It refers to all the pairs of products that you add together when multiplying two binomials.
Here is an example of this:
(2x + 3)(x + 5) = ?
- First: 2x * x
- Outside: 2x * 5
- Inside: 3 * x
- Last: 3 * 5
Adding these up gives:
2x2 + 10x + 3x + 15
Furthermore, because you are adding polynomials with like terms, you can simplify this expression further:
2x2 + 13x + 15
And that’s the final, reduced answer. You can apply the FOIL principle to any two binomials to arrive at their product. When you have more complicated polynomials, such as those composed of 3, 4, 5, or more monomials, you do the same type of thing. What I find easiest is to take the first term of the first polynomial, and multiply it with every term of the second polynomial. Then do the same for the second term in the first one, multiplying with every term in the second one, and so on.
Like this:
(x2+x+5)(x3+x2+1)
First group (multiply x2 with all in the second polynomial)
- x2 * x3
- x2 * x2
- x2 * 1
Second group (x)
- x * x3
- x * x2
- x * 1
Third group (5)
- 5 * x3
- 5 * x2
- 5 * 1
Now, you just add up all these terms, and simplify where you can:
(x2*x3)+(x2*x2)+(x2*1)+(x*x3)+(x*x2)+(x*1)+(5*x3)+(5*x2)+(5*1)
(x5)+(x4)+(x2)+(x4)+(x3)+(x)+(5x3)+(5x2)+(5)
(x5)+ 2(x4)+6(x3)+6(x2)+x+5
And that’s it. A little more complicated, but as long as you keep track of what you’re doing and work your way through it, you will arrive at the answer!

