Following my posts on How to Solve Quadratic Equations, you will soon find that not all quadratic equations can be solved by quadratic factoring, and you will come to rely on The Quadratic Formula to help you. As a quick refresher, a quadratic equation is one which takes the form of ax2 + bx + c = 0, as long as the “a” term is not zero. In other words, a quadratic equation is one in which there is an x2. (The “b” or “c” term can be zero.) I have already described the process you should follow if your question can be factored down, and you can express it as a product of two smaller expressions. Then, you can solve for two roots by letting each of the small expressions equal zero. I highly recommend reading my previous post if you need to go over this quadratic factoring technique.
However, as I said, not all quadratic equations can be solved this way. Sometimes, they are already expressed in a simplest form, or further manipulations just make things messier. In these cases, you can use The Quadratic Formula to solve for the roots of the equations. At first glace, the quadratic formula looks like a beast of a formula to use, and even harder to memorize! But, trust me… commit this formula to memory and learn how to use it, and solving quadratic equations will become so easy for you!
So, what is the Quadratic Formula?
I will go over how to solve it, but first, the it looks like this:
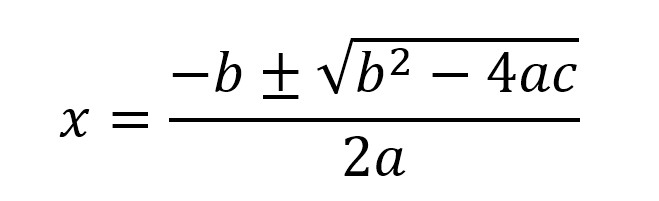
You can use this for any quadratic expression of the form ax2 + bx + c = 0, where “a” does not equal zero. (If you think about this condition, you can see that if a = 0, then there is no x2 term at all, and you are left with a linear equation or something of a higher order. Also, if a = 0, the quadratic formula then has 2(0) in the denominator, which equals 0 and causes the whole expression to be undefined. So, hopefully that short explanation will help you to remember that if a = 0, you cannot use the quadratic formula!)
Working through the math of the quadratic formula isn’t as difficult as you may think. To start, all you do is arrange your question into the form of ax2 + bx + c = 0, and then you can easily identify the coefficients for a, b, and c. Then, you simply substitute those values into the quadratic formula, and do the math. One thing to draw your attention to though is the “plus/minus” sign. Basically, the quadratic formula is really TWO formulas, one with a “-b + √…..” and one with “-b – √…..” These two formulas are what give you your two roots.
You will study this more in the future, but for now you may find it interesting that a quadratic equation, i.e. an equation with an x2 term, defines a parabola. The equation of all parabolas have x2 as the highest order exponent. As a result, you can imagine that a parabola drawn on an X-Y graph will cross the x-axis twice (at the most). These are the roots or solutions of the equation, and so that is why you cannot have more than 2 roots. Similarly, you can figure out why there may be 1 or even 0 roots, depending on where the parabola is located on the graph.
So, now that you know the answer to ‘what is the quadratic formula,’ next I will show you how to use it. Examples coming in my next post.

