A concept which may need a bit more explanation is: which average is appropriate for a given question? What is the best measure of central tendency? When would you use a median instead of a mean, or perhaps use a mode instead?
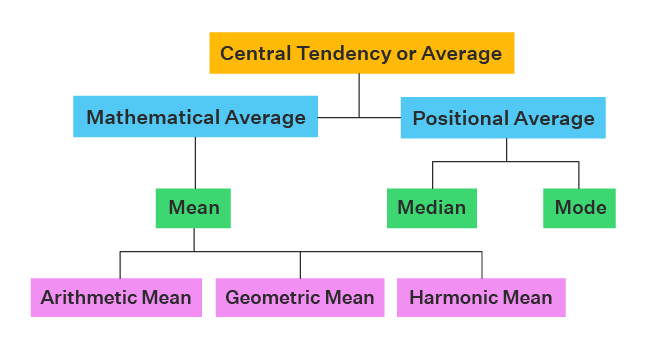
For any data set, you can perform the analysis to come up with a value for each average. However, here are a few basic guidelines to help you choose the most appropriate form of central tendency to describe your data.
1. For a normal, random distribution of data (evenly distributed), the mean is preferred.
2. For a skewed data set, a median is more appropriate than a mean. The skewed data set (ie. extreme data points) will cause the mean value to be much more extreme than the median, and therefore less central.
3. The mode can be used for non-numerical data. Eg. hair colour in a classroom.
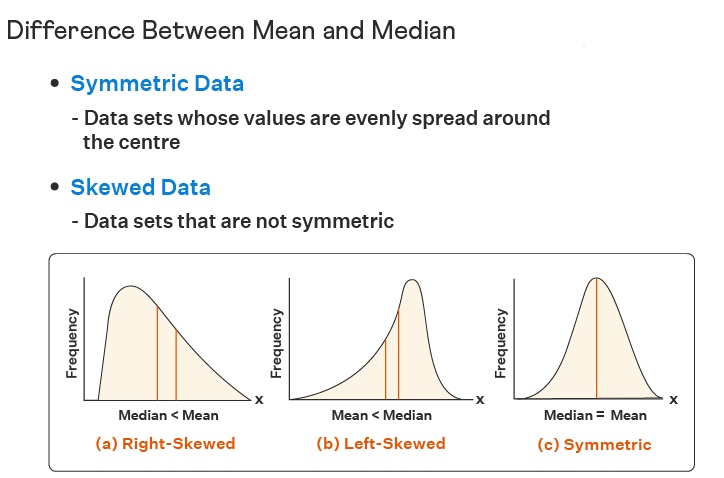
Here are a few examples of where each would be appropriate:
Mean:
- students’ heights in a classroom
- temperature over a length of time
Median:
- income of a group of people
- test scores for a group of students
Mode:
- finding the most common hair colour in a room
- finding the most common car in a parking lot
Hopefully these guidelines will help you to determine which is the most appropriate measure of central tendency to report for your data set.
