As I’ve discussed several basic concepts about functions and graphing to this point, now I want to build upon those lessons and explain some more complex concepts. In particular, I want to show you how you can modify a function in order to produce a defined change in its graph. Similarly, by the same idea, you can shift around your graph first and then be able to go and say how its equation has changed.This is a favourite topic of math teachers! The first graphing manipulation I will demonstrate is shifting graphs vertically, and then show you how to identify this transformation by looking at the equation. This is also called vertical translation.
Let’s look at a simple equation first:
y = x
This equation represents a line that goes through (0,0), (1,1), (2,2), etc. Now, what if I asked you to draw the graph represented by the new equation y = x + 2. Some students may suggest to make a table of values and then plot the points on the graph… never a bad way to do things, but not necessarily the easiest.
Let’s think about things SLIGHTLY differently. In the first equation, let’s think about y specifically as being the height (and not just a different variable), and so the height for a given x value will always be equal to that x value. Not a huge change in our thinking, but it may help some to see graphical changes easier. Now, let’s apply this thinking to the second equation, and we see that the height is always going to be 2 greater than the x value.
Now, let’s spice things up a bit. Let’s look at a function. (The solution to the function for each value of x is similar to what y would be for each value of x in a regular equation).
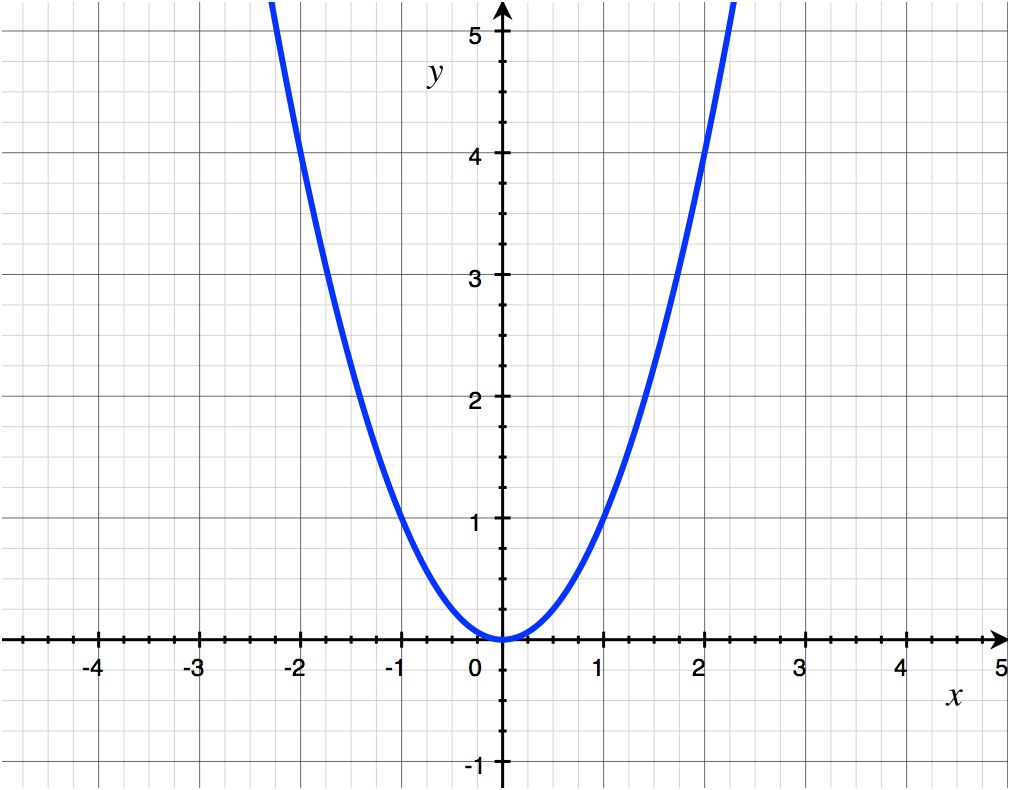
f(x) = x2
You may recognize this equations as being a basic equation that describes a parabola that opens up. The lowest point on the graph is (0,0).
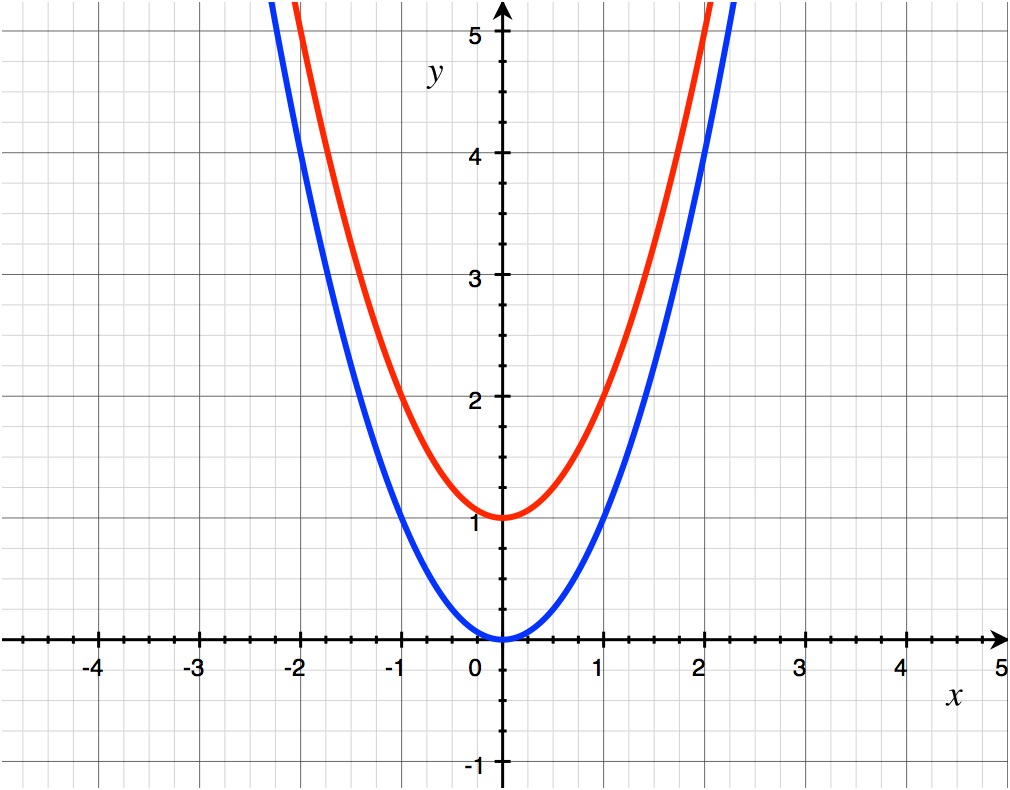
Now, if I said to draw the graph of f(x) = x2 + 1, apply the same type of logic, but keep in mind one VERY IMPORTANT THING. The “change in height” is dictated by the single number that is not associated with the x variable… this may be clearer after another example, but let us focus on this one for the moment. You should hopefully be able to see that this change in our graph will result in a shift up of 1 unit, shown by the red curve below alongside the original blue one from above.
One final example, hopefully to clear things up for good. Consider a more complicated function, alongside a slightly modified version of it:
f(x) = (x-4)3 and f(x) = (x-4)3 + 5
So, after those examples, here is the takeaway message that hopefully is the ray of light for you.
Picture all the complex stuff that is happening to x as being one “chunk” of the height component, and then when you add the “+ 5” to the equation, you are really just adding an additional “height chunk” to the total height for a given x. So in the end, the second equation above looks exactly like this one, only shifted 5 units up:
Remember to combine terms if necessary, so that you are left with a single number to add to the x term (and whatever operator is acting on it). You will quickly find that vertical translations of graphs are far simpler than they may sound at first!
