Trigonometry is the type of math that you use when you want to work with angles. Luckily, some angles are used so frequently that they have their own dedicated name and shortcuts that you can memorize. These are called special angles in trigonometry, and you can use special angle triangles to help.
Special angles are great to know because their trigonometric functions equate to very specific and known ratios, so if you can memorize these it will save you a lot of time in doing trigonometry homework! To make things a bit easier, if you can’t remember these exact values, it is even easier to memorize the special angle triangles that these angles are based off of! And there are only two triangles, so you will find that it is very easy to derive the trig functions if you can’t remember them.
Specifically, the trig functions are easy to find for these special angles, which are: 0, 30, 45, 60, and 90 degrees.
45-45-90 Triangle
This will hopefully make sense after looking at the triangles I mentioned. Here’s another site that also talks about remembering the patterns of these triangles instead of specifically remembering the math. Create a right angle triangle with two 45 degree angles, and with two sides of 1 unit length. By using the Theorem of Pythagoras, you can find that the hypotenuse of this triangle is easy to calculate to be length √2. This is what this triangle looks like:
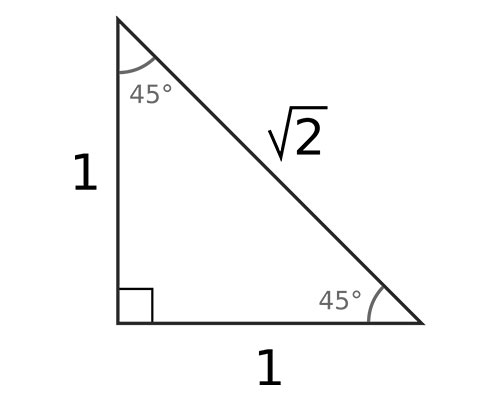
So then, from these values and using the memorization trick of SOHCAHTOA, you can obtain the trigonometric values for this special angle of 45 degrees. You can work out that:
Don’t worry if you can’t remember these values and ratios. The easiest way to remember them is to memorize how to construct the special angle triangle. And as you can see, this triangle is very simple: a right angle triangle with a 45 degree angle and 2 sides of length 1, and you can easily fill in the rest and then work out the ratios yourself.
30-60-90 Triangle
The second of the special angle triangles, which describes the remainder of the special angles, is slightly more complex, but not by much. Create a right angle triangle with angles of 30, 60, and 90 degrees. The lengths of the sides of this triangle are 1, 2, √3 (with 2 being the longest side, the hypotenuse. Make sure you don’t put the √3 as the hypotenuse!). FreeMathHelp also has a good explanation of this particular triangle. This triangle looks like this:
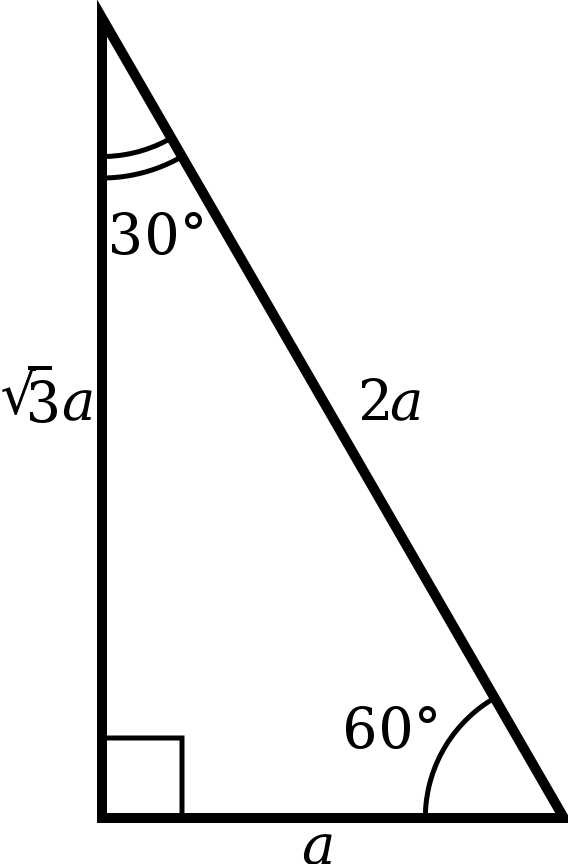
Here are the trig ratios that you can easily find:
Once again, just remember the triangle, and the ratios are easy to derive!
For 0 and 90 degrees, there isn’t a triangle to remember (although please feel free to correct me if I am wrong!), so you will actually have to memorize these values. However, these aren’t complex. I usually just remember the pattern of the following list:
If you can’t memorize the actual trigonometric ratios for the special angles, the key is to recall the special angle triangles that describe them. Make sure that you know how to construct the triangles, and then you can solve the trig ratios of the trigonometry special angles. You will quickly find that doing trigonometry questions that use these special angles are easy!

