The trig functions that I’ve discussed so far (Sine, Cosine, and Tangent) will be incredibly useful to you when working specifically with right angle triangles. However, of course, not all triangles have a 90 degree angle in them. So can you still use these functions? Well, yes, but in a different way. One way is through application of the Law of Sines.
Let’s consider a triangle that has three different angles, none of which are right angles. The standard naming scheme still applies, although now there is no hypotenuse (remember, the hypotenuse is opposite to the 90 degree angle).
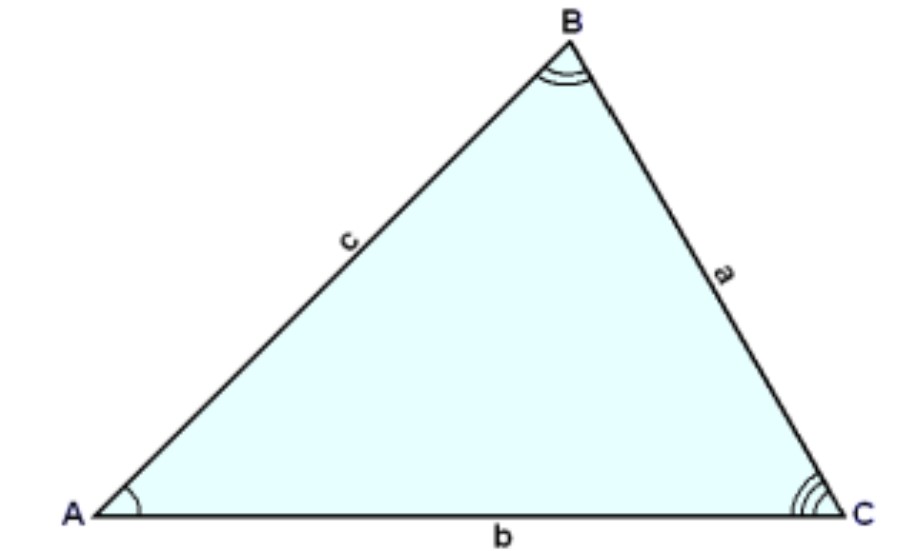
So, now we have our triangle, what is sine law? This trigonometry sine law says that the ratio between the sine of an angle and the side opposite to it will be equal for all three angles. In other words:
So let’s try some sine law examples. Say we have a triangle with 1 known angle of 40 degrees, sides 4 and 6 units long. Find angle B:
The Sine Law says that the ratios of angle to opposite sides will be equal. With this, we know how to find an angle using sine law. So we have:
6 x (Sin 40) = 4 x (SinB)SinB = 0.964B = 74.62 degrees
Now, if the question had asked to find all the angles in this triangle, an easy trick you can apply at this point is to simply say that since the 3 angles in the triangle will add up to 180, you can just subtract your known angles from 180 to get the third angle:
180 = 40 + 74.62 + C
C = 65.38
And now that you have angle C, you can use the Law of Sines with that angle to solve for the final unknown side:
cSinA = aSinC
c x (Sin 40) = 4 x (Sin 65.38)
c = 5.66
Whenever you are given a triangle that does not include a right angle, but you are provided with 1) an angle, 2) the length of the side opposite to that angle, and 3) any one of either the other sides or angles, then you can use the Sine Law. Now you know how to find an angle using sine law!

