The Cosine Law works similarly to the Sine Law that I have already discussed. Actually, it may seem somewhat familiar to you. While the Cosine Law can be used on any triangle, the Pythagorean Theorem is a specific case of the Cosine Law which strictly applies to right angle triangles. It’s a bit more of an equation to remember than the Sine Law unfortunately, but it is extremely useful. Here is the equation:
c2 = a2 + b2 – 2ab cos C
Upon a quick analysis, you can see that this law requires two of the three sides in a triangle, as well as the angle opposite the unknown side (or the angle contained by both of the known sides) to provide you with the unknown third side. Here is another trick to think of it: use your thumb and index finger to form a V shape that will represent your triangle, and if you know the lengths of the two sides (fingers) and the angle between them, you can find the remaining side by using the Cosine Law. This is useful for finding the third side of any triangle when two sides and the angle between them are known.
Let’s try an example, where we will solve for the unknown sides and angles.
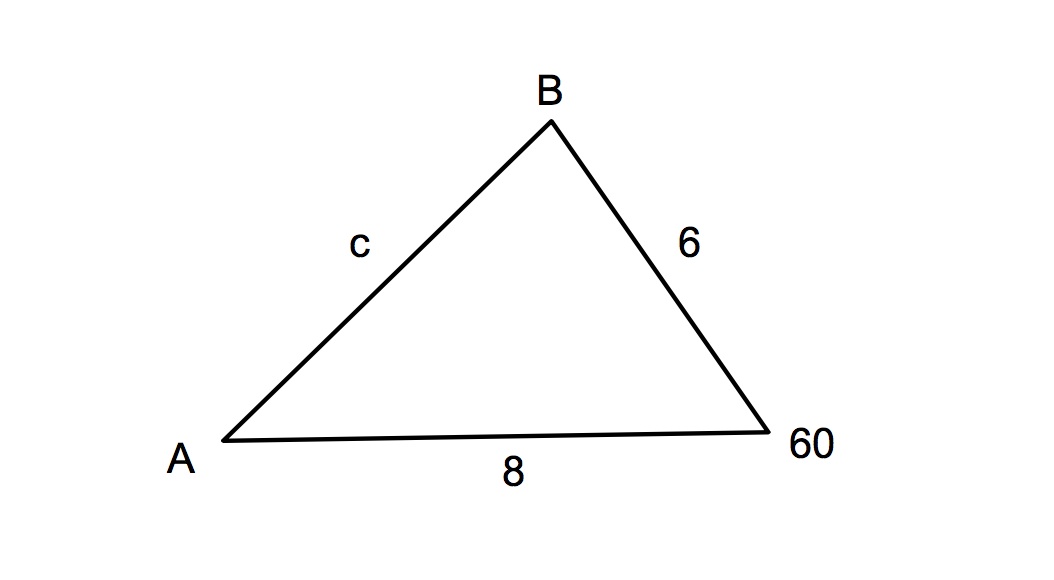
First, assess the information that you are given and come up with a strategy to solve this triangle. (The phrase “solve the triangle” is often used to instruct you to determine all of the missing angles and sides). In this case, there are two sides and the angle between them known – the perfect case for the Cosine Law to deduce the unknown side! Once we’ve gone that far, we will have then obtained a complete ratio (side and angle) to use in the Sine Law to solve for the remaining two angles. So, now let’s put our strategy to work!
So by the Cosine Law:
c2 = 62 + 82 – 2(6)(8) cos 60
c2 = 36 + 64 + 96 cos 60
c2 = 36 + 64 – 48
c2 = 52
c = 7.2
Now that we have done that, we have obtained the final side length, and therefore a complete side/angle ratio to use with the Sine Law! And now, you can find the rest of the angles to fully describe the triangle!
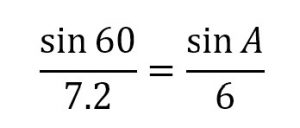
and
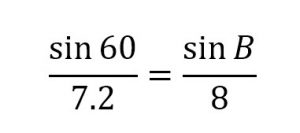
I’ll leave those for you to solve. But that’s it! Using a combination of the Cosine Law and Sine Law, you can completely solve any triangle that you are given. These are extremely powerful and useful equations!
Also, on a side note… as I mentioned at the start of this post, the Cosine Law is a generalization of the Pythagorean Theorem, which specifically applies to right angle triangles. You can see that if you are working with a right angle triangle and substitute in 90 degrees to the Cosine Law, it reduces down to the Pythagorean theorem:
c2 = a2 + b2 – 2ab cos C
but
cos 90 = 0
so
2ab cos (90) = 0
reduces to 0, and so
c2 = a2 + b2
The Pythagorean Theorem!

