The Theorem of Pythagoras is a specific case of the Cosine Law that applies specifically to right angle triangles. With it, and given any two sides of a right angle triangle, you can find the third side. Then having solved all the sides of the triangle, you can use the standard trig identities (Sine, Cosine, Tangent) to evaluate the sizes of all the angles. Therefore, you can see how incredibly useful this very well-known mathematical theorem is! Let’s look at it in a little bit more detail.
The definition of the Theorem of Pythagoras states that the square of the hypotenuse is the sum of the squares of the other two sides. That’s the wordy version, but it’s all you need to remember how to use it. Personally, I can almost recall this phrase even more easily than the mathematical expression that defines it, and that is a very simple equation to remember! This is how quick and painless the formula is:
c2 = a2 + b2
That is all there is to it! This is known as the Pythagorean Equation. It’s amazing that such a small equation can have such a wide-reaching application. This expression says exactly what I defined above, as it provides a simple relationship connecting the three sides of a triangle. The only condition required is that we have a right angle triangle, with c in the expression being the length of the hypotenuse. So then we have the square of the hypotenuse (c) equal to the sum of the squares of the other two sides. If you think about this relationship, you can also deduce that the hypotenuse will always be the longest side, and always less than the sum of the other two.
Now you might be wondering just WHY this equation is true. Perhaps you want proof. OK then, here is a diagram to prove this to you. What I have done is created a right triangle with sides a = 3, b = 4, and c = 5, and then built a square off of each of the triangle’s sides. (Get it? I squared each side!) If you do the math, you will find that the sum of the area of the side square and bottom square (a and b) are equal to the area of the square built off the hypotenuse. Visually, this is all that the math means.
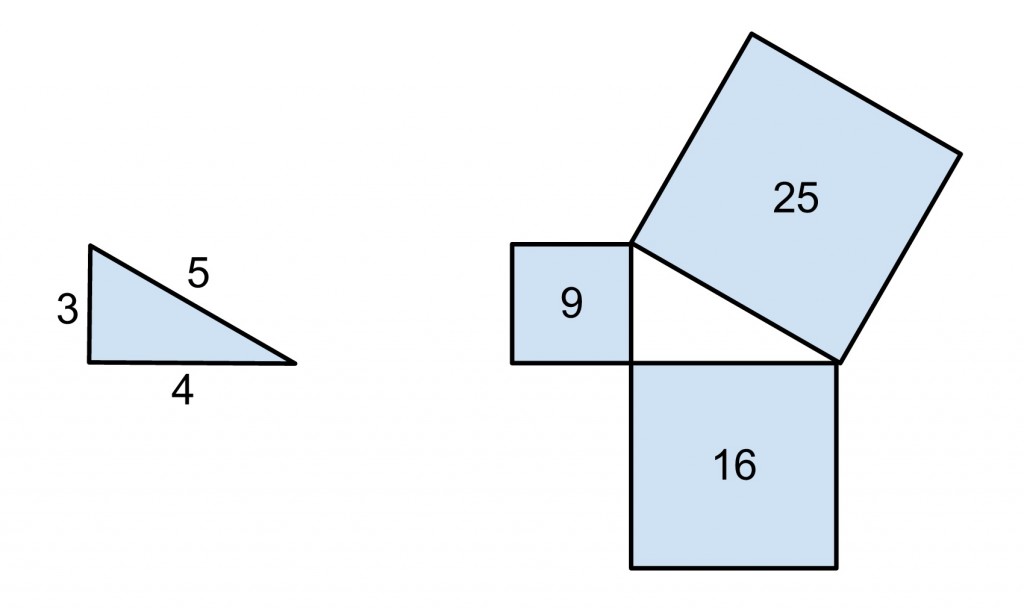
Hopefully, the diagram above is sufficient enough to demonstrate this concept. However, maybe you would prefer to see video proof that a2 + b2 = c2? Here is a fantastic video that I found that perfectly demonstrates this theorem. It is a wonderful, watertight demonstration of the theorem of Pythagoras that shouldn’t leave you with any doubt.
Here’s another page with a thought exercise on it to prove the theorem. This Pythagorean card table problem is another good demonstration of putting these mathematics concepts to good use!
This is one of the most basic trig concepts, and is probably one of the first concepts that were taught in trigonometry. In fact, there are several different variations of proofs that have been developed over the years, based on concepts of proportionality (similar triangles), geometry (Euclid’s proof, or rearrangement), or algebra and calculus. It is very important and very useful, as you will undoubtedly be able to make use of it in a wide range of solutions to math questions for years.
