Solving trigonometry problems can be easy, but it first requires you to have a solid understanding of the basic trig functions. There are three of these functions, and the first one I will discuss is SINE. In subsequent posts, I will highlight the other two functions: cosine and tangent.
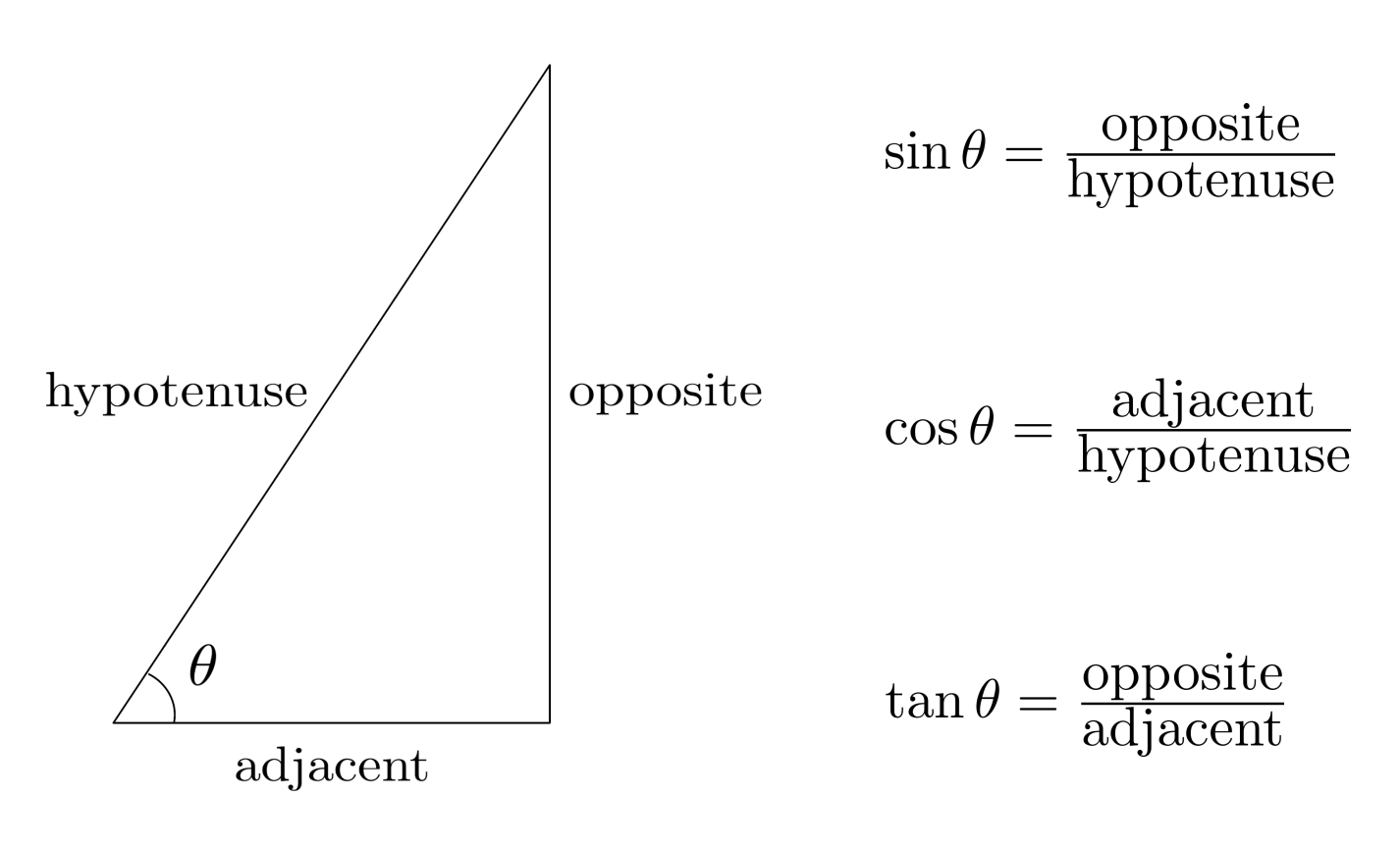
The sine definition relates an angle of a triangle to the ratio of its opposite side and the hypotenuse. So, if we look at angle B in the picture below, (and keeping in mind the notation for sides), we can see that SinB = b/c.
In more general terms, SinB = opposite/hypotenuse. We write “Sin” as the shorthand form of Sine. (Sounds like mathematicians are kind of lazy… since it appears that writing 4 letters was too much, they had to shorten it to 3!)
Similarly, SinA = a/c. Again, it is opposite/hypotenuse… remember how I said it was important to understand the RELATIVE notation scheme! If you need a refresher, take a look at my prior post that goes over triangle naming conventions.
SOHCAHTOA is the trig acronym that describes the three basic functions and their ratios. It may be easier to remember if you look at it with spaces: SOH CAH TOA. The one that we are interested in this post is the SOH term, which is short for “Sine is Opposite over Hypotenuse.” There are many other mnemonics that can be used to remember the order of these relationships, and to help make this a more fun post, I encourage everyone to leave their favourite memory trick for SOHCAHTOA in the comments below. There is no one right way to have soh cah toa explained. Whatever works for you to help you remember is all that is important.
Working with the Sine function is fairly straightforward, and usually just a matter of plugging the appropriate numbers into the ratio.
For example, you can imagine a triangle with known side lengths, and be asked to find the angles. This is a very common and simple question that you will get. In this case, you would say Sin(B) = opposite/hypotenuse (where you substitute in the known values for the sides.) This will give you Sin(B) = “some value.” And now, just as in working with addition or multiplication, when you want to solve for a specific variable, you have to isolate it… and to isolate it, you must do the same thing to both sides. Therefore, to get rid of the Sine, you must do ‘inverse sine‘ to each side (which is usually the same calculator button, but pushing SHIFT to access it). Then you’ll get B = inverse sine of (some value), which is your answer. Technically, you are taking the arcsine of the ratio.
Similarly, if you know a mixtures of some of the sides and some angles, you may be asked to find the unknowns. You can then say Sin(known angle) = opposite/hypotenuse (where one of these sides is known and the other unknown), and then just simply solve for the unknown side length.
Here’s a quick 3-4-5 triangle example:
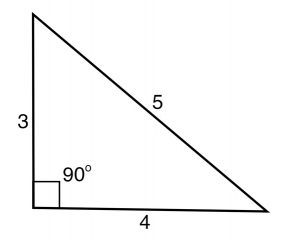
So from this triangle, using the sine definition, we can tell that:
SinA = (4/5)
SinA = 0.8 (now push inverse sin on your calculator…)
A = 53.13 degrees
Also:
SinB = (3/5)
SinB = 0.6
B = 36.87 degrees
A useful trick for quickly solving triangles is to understand that if you sum up the three angles, they will always total 180 degrees. So for this triangle, after solving angle A, you could subtract it and 90 from 180 to find B. Of course, this defeats the purpose of practicing Sine in this example.
On the other hand, if we already knew that angle B = 36.87 degrees, and we wanted the length of the unknown hypotenuse, then we do:
Sin(36.87 degrees) = 3/hypotenuse
0.6 = 3/hypotenuse
hypotenuse = 3/0.6 = 5
As you can see, there really isn’t anything complicated about performing these steps. For the most part, it’s simple arithmetic with a few things about triangles thrown in for good measure. I hope this explains the sine definition so that it is understandable, and I also hope that now that you have had sohcahtoa explained, that makes more sense too. As always, please don’t hesitate to comment if you’re unsure or if you would like additional help. I’ll discuss cosine and tangent in the next few posts.