One of my previous posts introduced you to functions and how they work, but there are few other things worth discussing that I would like to add here. The first is more about function notations, then I will expand that into a demonstration of complex functions, and then wrap up this post by introducing the concept of piecewise functions.
When I introduced functions, I referred to the standard notation as f(x). However, you will quickly come across problems that use different letters – this means the same thing. You will probably see things like g(x) or h(x), and they are just used to differentiate between different functions. For example, consider the following functions:
f(x) = 2x + 3
g(x) = x – 8
h(x) = 4x + 1
This shows that the functions f(x), g(x), and h(x) are equal to the given expressions. So f(x), g(x), and h(x) all represent different functions (continuing the metaphor from earlier, these are all different “machines” that act on your input to produce their specific outputs). The f, g, and h are all essentially saying the same thing – that is, they are the names of their function. It’s comparable to saying 3x = 12, or 3a = 12… the underlying math is the same, though in this case, the name of the variable is different. Same thing with function names.
So, now that you know how to differentiate between and name different functions, we can do slightly more complicated things – things like complex functions. If for the following function we want to solve f(1), we substitute 1 in for x, and solve it to get 5:
f(x) = 2x + 3
f(1) = 2(1) + 3
f(1) = 5
However, we can now ask for something more complex such as f(g(x))… read as “f of ‘g of x’.” Looks complicated, but keeping in mind what the function notation is saying and what a function is actually doing, we can easily solve this by substituting the expression for g(x) in for x (instead of just subbing in a single number like before). Continuing our metaphor, it’s like saying that our function machine f(x) has an input of the entire machine g(x).
f(x) = 2x + 3, g(x) = x – 8
f(g(x)) = 2(x – 8) + 3
f(g(x)) = 2x – 16 + 3
f(g(x)) = 2x – 13
Furthermore, if we wanted to solve f(g(5)), we can do one of two things. We can evaluate the expression as we just did, then solve when x= 5 (like I said above, this is like giving the f(x) machine the entire g(x) machine as its input. It’s a machine working on a machine working on a value!). Or, we can solve g(5) first, then substitute that into f(g(x)) – basically, starting at the inside and working your way out to the outermost function (that is, we provide the g(x) machine the input of 5, get the output for that, and then give that to the f(x) machine as its input). Both methods will get you the same answer, and it’s really up to you to do whichever you are most comfortable with (unless you are instructed to specifically do one way or the other!).
Method 1:
f(g(x)) = 2x – 13
f(g(5)) = 2(5) – 13
f(g(5)) = (-3)
Method 2:
g(x) = x – 8
g(5) = 5 – 8
g(5) = (-3)…
then…
f(x) = 2x + 3
f(g(5)) = f(-3) = 2(-3) + 3
f(g(5)) = (-3)
Both methods get the same answer, because they are doing the same things. It’s just a matter of what you are more comfortable with. Function notation can get very confusing like this, but for problems like this, you just have to basically work from the inside out, just as in any other math expression you’ve seen! (eg. (2x + 7(3x -4) + 2)…. solve the inside bracket first, then the outside). They may seem tricky, but you will be surprised at how easy they are when you see through the notation and know what they are asking!
Now that I’ve explained complex functions, I’d like to expand on this to discuss what is known as piecewise functions. I’ll post a follow-up shortly to focus on graphing piecewise functions, but here is an introduction to them.
The functions that I’ve discussed so far (and generally, what most people typically talk about) can be drawn as continuous, smooth curves with no gaps. These tend to be described by a single equation. But what if you consider a graph that is composed of two distinct sections – such as one with a rising diagonal line attached to a horizontal line at the top? Taking each section on its own, you can imagine how it would have its own unique equation. However, combining these sections into graphs such as these, which are described by multiple equations each applying to specific domains of the entire curve, these are called piecewise functions. Obviously, they get their name from the fact that the function is made up of several “pieces”. Here is an example of what a piecewise function would look like on a graph, as well as how you would express this type of function mathematically:
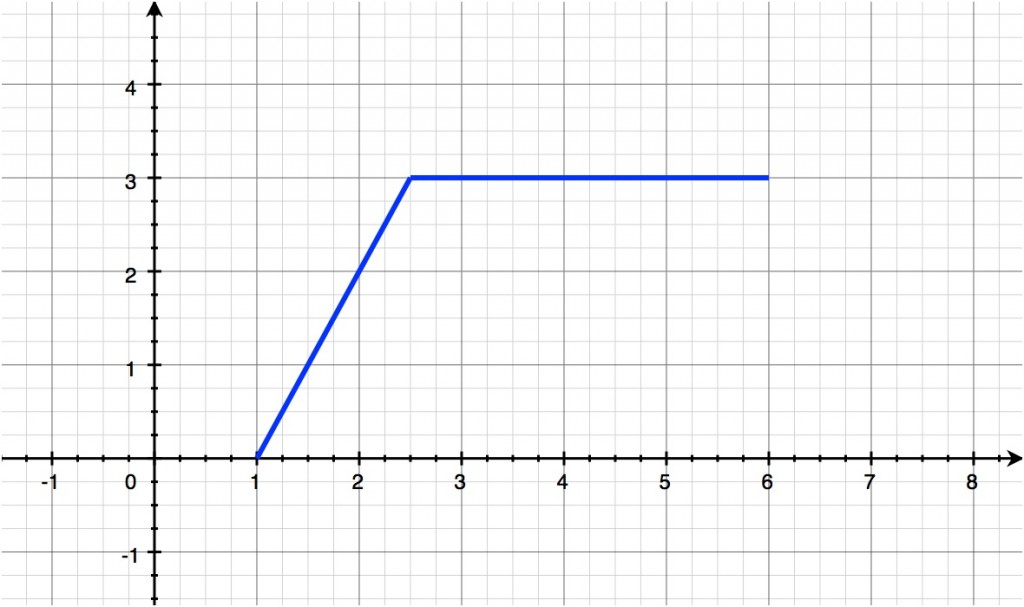
![]()
The notation basically says that here is the function f(x), and it is equal to the listed equations over the specified domains. So here, f(x) is equal to 2x-2 only across the domain that is between 1 and 2.5. Similarly, f(x) is equal to 3 when the domain is between 2.5 and 6. In this case, at the point on the curve corresponding to x = 2.5, both equations are valid and will produce the same value. However, it is important to pay attention to the “greater than” and the “greater than or equal to” signs, depending on what your particular question is talking about.
With that, I will conclude my brief introduction to complex functions and piecewise functions, and I will look ahead to my next post where I will go into a bit more detail about graphing piecewise functions and some things to keep in mind, as I have hinted at above.

