Logarithms sound like very advanced math concepts, but they’re not really that much more difficult than many other mathematical concepts. The word “logarithm,” like the word “algorithm,” gives the impression of being a very complex topic. However, much like how an algorithm is nothing more complicated than a set of rules or processes to follow, a logarithm can also be very easy to work out. The first step to clearing up any confusion, though, is to explain what is a logarithm?
So then, just what is a logarithm?
A logarithm is related to exponents. Actually, it’s kind of like working backwards with exponents. A logarithm (or “log” for short) of a number is the exponent that another value (the base) must be raised to equal that number. Still sounds complicated, right? Looking at it another way, a logarithm tells us how many of one number we multiply together to get another number. That sounds a bit more manageable. Now let’s look at an example so that you can really see how easy this is.
Let’s consider the number 81. How many 3’s do we multiply together to equal 81?
3 x 3 = 9
3 x 3 x 3 = 27
3 x 3 x 3 x 3 = 81
As you can see, and easily work out yourself, you multiply 3 four times to produce 81. Another way to write this is with exponents, like this:
![]()
Now, what does any of this have to do with logarithms? In this example, we can say that the log with base 3 of 81 is 4. Or, as we found above, we multiply 3 (our base) 4 times to get 81. It is more common to say this as “the base 3 log of 81 is 4.”
What would a new math concept be without introducing a new expression? Of course there is a simple way of writing this down on paper, rather than longhand with words. Here is what our expression looks like:
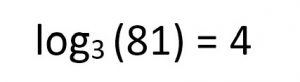
Let’s compare our two expressions (the exponential notation and the log notation), and then I will show you a trick to help you work with them. This trick got me through years of logs in school! Notice first that all of the numbers are used in both expressions, though they’re in different places. In this case, the 3 is the base value, which is raised by the exponent 4 to produce the result 81. Similarly, with the logarithm notation, the base value is again 3, and we want to know what number this base is raised to give our results of 81. So, as you can see, the solution to the logarithm actually tells us what the exponent is!
Here is the simple arrangement of these components that help when working with logs. It can basically be boiled down to a simple rearrangement. The 3 moves over and bumps the 4 up to the exponent level, you remove the “log” word, and you’re left with your exponential notation of the expression.
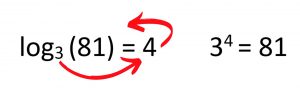
Hopefully this post has helped you to understand what a logarithm is, and how logarithms are related to exponents. As I explained at the start, the concept is not that difficult. Now, much like the exponents they are related to, there are a bunch of rules that you need to follow when doing any kind of mathematical operations involving them. In my next post, I’ll begin to explain some of these logarithm rules.
Thanks for reading my post! Please remember to like me on Facebook if this was helpful for you. Of course, as always, feel free to leave me some feedback in the comment below.
