In this post, I would like to elaborate a bit on the concept I presented in a previous lesson. Specifically, I’m going to go over graphing piecewise functions. There are a few conventions that are important to keep in mind when graphing these. Today I will explain these points and show you additional examples of different variations of piecewise functions.
But first, let’s recap!
In general, a piecewise function may be considered as a function that is described by more than one equation, with each equation only being applicable to the function over specific domains. So, this is like saying you have a line that rises to the right on a graph across the domain of x = 0 and x = 3, and then the line falls to the right from x = 3 to x = 6. The upward sloping line is described by one equation, and the downward sloping line is described by its own different equation. (A point of interest in this example is at x = 3, where both equations apply!)
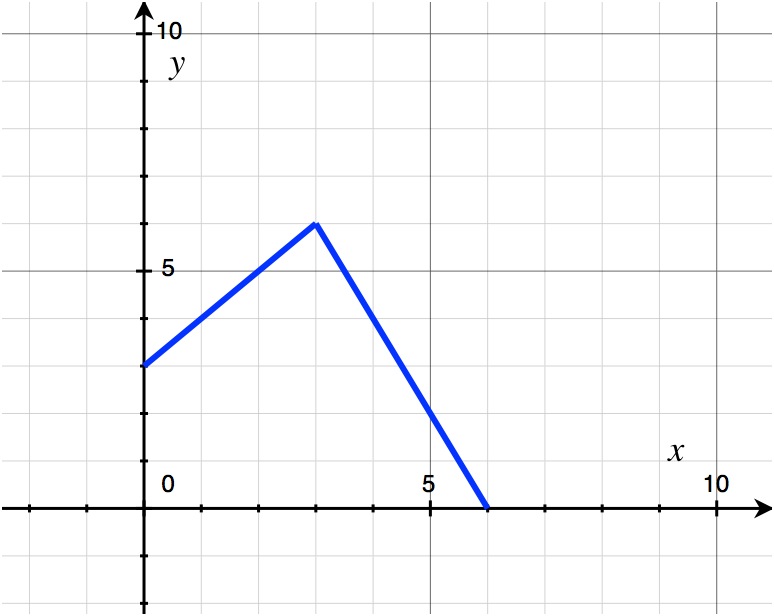
Together, these two lines form the graph of our function. (I realize that the vertical axis should be labeled as f(x) rather than y, though I can’t seem to find the setting to change this in my graphing program…) A seemingly complicated mathematical curve like this is bound to be expressed as a complicated looking set of equations, right? Well, as I outlined in my introductory post, it’s not that bad when you know what you are looking at.
You basically express a piecewise function as a list of equations, grouped one on top of the other to the right of an open parenthesis.
At first it looks complicated, but it is really just two equations, with their domains explicitly noted. (Actually, piecewise functions can have many equations in a list, though I will just work with two for simplicity!) In this example, you can see that there is a positively sloped line that spans the domain of 0 to 3, and a negatively sloped line that spans the domain of 3 to 6. In this case, as I have created this question, the vertex of the graph is a solution to both equations, which I indicated in the problem as the greater than or equal signs. So, if you want to know what f(3) is, you need to assess the piecewise components to see which equation you need to solve in order to arrive at your solution. In this case, both equations are valid when x=3, so you can solve f(3) using either one. You will find that indeed each equation will provide you with the same output.
That was a fairly standard example of graphing a piecewise function. However, you can also have a piecewise function that isn’t continuous.
In this case, you can see that my function is composed of two line segments. The first part is the line f(x)=3, over the domain from zero to 3. However, pay attention to the greater than signs! Here, the lower limit is greater than or equal to 0, though the upper limit is where x is less than (not “or equal to!”) 1. In situations like this, you denote this on the graph with an open circle around that point. This implies that you are including all of the points along the curve up to the precise point that is specified. So, in this graph, when x =1, you have to abide by the second equation, because that is explicitly given in the domain of the second equation. However, at x = 0.99999999999999, you fall within the domain of the first equation. So, pay attention to your signs! If your test question here said “what is f(1)?”, if you answer as f(1)=3, you would be wrong! It is a simple mistake to make, so it is best to really pay close attention! Making the mark on the graph will help you to not get mixed up by simply looking at the signs in the expressions.
Another graph notation to keep in mind is to explicitly express points on the line as “greater than or equal to”. You can do this by marking with a filled circle. Often, you won’t actually have this shown, as it frequently is just understood that if there is no open circle, the point is included (as I have done above). However, it is wise to understand that there are two ways of marking points on a graph – a filled circle includes the point, but an open circle means getting infinitely close to the point but never exactly including the point. These are important notes and are favourites for teachers to put on exams!
A final brief note I will include here is a refresher on the convention for expressing domains (also applicable to ranges), known as interval notation. As I show above, the first part of the expression is f(x) = 3 when x is greater than or equal to 0 and less than 1. This is awfully wordy for mathematicians! So obviously, there is a better way to denote this, and it is done by using brackets. The convention is that if the greater than (or less than) includes “or equal to”, you use square brackets, like this: [ ]. If there is no “or equal to” then you would use round brackets, like this: ( ). The left bracket refers to the lower/left limit of the domain, whereas the right bracket refers to the upper/right limit of the domain. Inside the brackets, you include the lower and upper limit of the domain, separated by a comma. So, for this example, we could simply express the domain of this first part of this piecewise function as [0, 1). Similarly, the second part of the function can be denoted as [1, 5]. Of course, both brackets do not have to be the same – each one is completely dependent on what the sign is telling you. So you can have [ ], ( ), [ ), or ( ]. This is a great shortcut to help you to express your domains and ranges, and it really comes in handy when graphing piecewise functions. The only piece of advice I can add is make sure your square brackets don’t look like round ones and you get confused!

