When working with functions in mathematics, one problem you will frequently be asked is to find the domain of a lineor identify domain and rangeof a graph. This is a relatively simple problem to solve, once you know what is meant by these terms. If not, you might first ask “what is domain and range?” This post will explain these concepts for you.
The domainis simply all the values of x that a function can take, whereas the rangeis all of the values of y that the expression can have. A different way to think of this is to consider that domain is horizontally where the graph is located. If you were to take a graph and squash it down to a single horizontal line, what values on the x-axis would it include? Similarly, the range is vertically where the graph is located, and if you were to squish a graph from the left and the right into a single vertical line, what values on the y-axis would it include?
Another important problem you will have to work with is to determine if a given graph is a function or not. This is also a much simpler question that many people first think. The key to solving this type of question is to use the vertical line test (take a look at Khan Academy for a good explanation of this test). If you have a function and you substitute in a value for x, you will only get one y value. A function won’t give you more than one value for y. If it does, it isn’t a function at all! The vertical line test is a very quick and visual way of working with this principle. To use it, you simply draw a vertical line through any point of your graph. If the vertical line only passes through the line at a single point, then it is a function. That is, the value of x corresponds to only a single value of y. However, if the vertical line passes through more than one point (for example, a circle), then you do not have a function because for a value of x, there is more than one value of y.
So, now you know how to use the vertical line test to determine if your graph is a function or not. Once you have decided that your graph is actually a function, you can then move on to finding the domain and range of a line. Assuming that your line is plotted on a graph paper already with labeled points, finding the domain of a graph is incredibly easy. All you have to do is identify the horizontal ends of the line, and say that the domain is between the left point and the right point. The same strategy can be used to find the range of line graph. An important note to make is that sometimes a domain or a range do not have end points, and so we say that they extend to infinity.
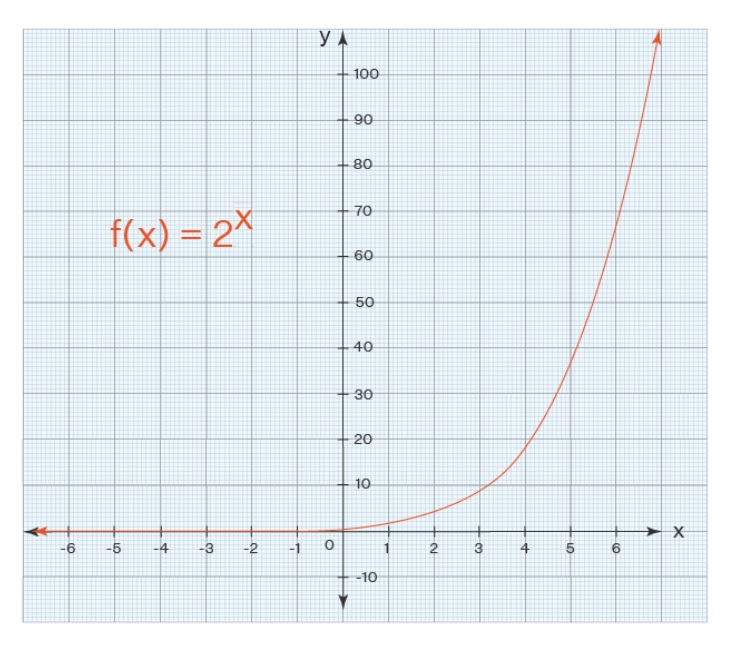
Domain and range of f(x)=2x
For example, if I asked you to find the domain of a line f(x) = x + 1, you can easily graph a straight line with a slope of 1, a y-intercept of 1, and the line extends forever up to the right, and down to the left. This particular line has a domain of negative infinity to positive infinity. So does the range. However, if I just drew a straight horizontal line, starting at the y-axis and extending to the right to x = 5, then you would say that the domain is between 0 and 5.
Another point to make is about the notation used to describe the domain and range. If the domain includes all of the numbers up to a point INCLUDING the point, then you use a square bracket [ or ] to represent that. On the other hand, if the domain includes all values approaching a point, but NOT the actual point itself (you will find this situation more when working with limits and calculus), then you use round brackets ( or ). So, for the previous question, I would record the domain as [0, 5] to indicate that the line extends from 0 to 5 and includes both of those points. If it didn’t include one, or either, of the points, I would use a round bracket next to the particular number. On the graph, if the line only approached a point, this would be represented by an open point, like an ‘o’.
When you advance to higher levels of graphing in algebra or calculus, finding the domain of a function will be a little more complicated, especially when you are looking at points that are irregular and cannot be precisely identified simply by looking at them. Piecewise functions are also a concept that will really require you to understand domains. However, I hope that by having domain and range explained here, it has given you at least a basic understanding of these very important math concepts, and with practice you will become an expert at finding the domain and range of a function.

