In my previous post, I introduced you to one of the most fundamental, basic concepts of trigonometry: the sine definition. I explained to you what exactly it is, and how it can be used. Similarly, there are a few other basic trigonometry functions that you need to know so that you can solve these types of problems. In this post, I will introduce you to a very similar and related trig function: the cosine definition.
The cosine definition is actually just as simple as the sine definition, though you need to keep straight which is which. Let me first show you what cosine means (the abbreviation for cosine is just “cos”), and then I will reiterate the trick so that you don’t confuse these similar math functions!
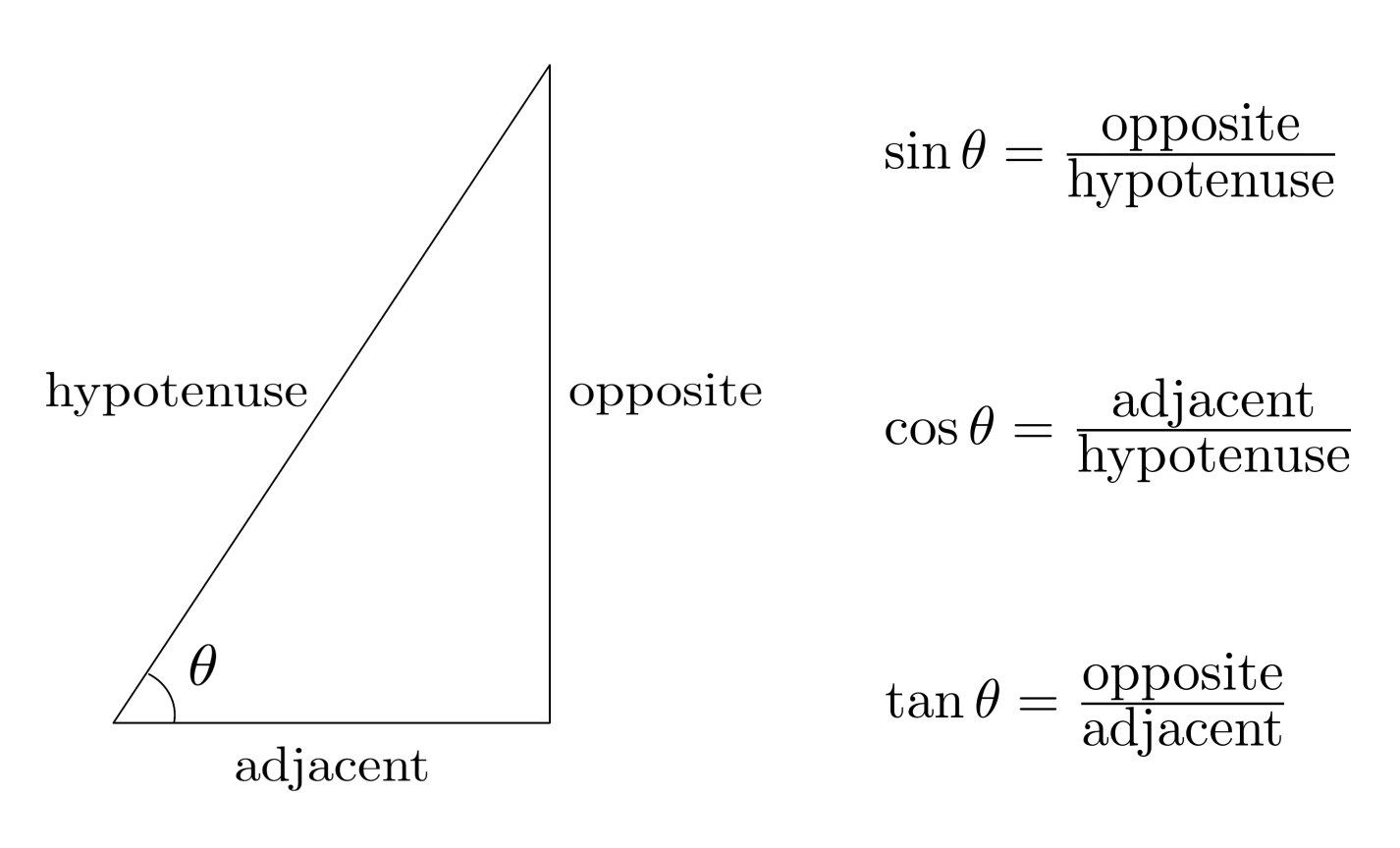
The cosine of an angle in a right angle triangle is quite simply “the ratio of the length of the side adjacent to your angle and the length of the hypotenuse.” That’s all there is to it: a ratio of two numbers. Of course, the trick is remember which two numbers are specific to cosine. The good thing is that in a triangle, there are only three sides to choose from. But more importantly, there is a very easy memory trick so that you will never mix the ratio up with the sine ratio.
As I mentioned in my last post, this great memory trick I’m talking about is to just remember this completely made-up, nonsense word: SOHCAHTOA.
(MathsRevision has a pretty good trigonometry page that explains this concept similarly, with a different example and a short video).
If you break the word into its three components, you will understand quickly why this word is so great. Remember how the word sounds, then just put a space after every three letters, which gives you three words made up of three letters each: SOH CAH TOA.
The beauty of this word is that it tells you all you need to know about the three basic trig angles. The first letter of each component refers to the trigonometric function, and the following two letters represent the names of the sides that are involved in that ratio.
The key to understanding this is to remember the triangle naming rules, and what is meant by “opposite” side, “adjacent” side, and “hypotenuse.”
So what does SOHCAHTOA tell you? It tells you that “Sine is Opposite over Hypotenuse” (see the first letters? S.O.H. = Sine Opposite Hypotenuse). Similarly, it tells you “Cosine is Adjacent over Hypotenuse.” I’ll leave the last part for my last post in this three part series, but I’m sure you can figure it out pretty easily now.
So, there you have it! Now you understand what is meant by the cosine definition, how it applies to your trigonometry homework, and how to use it. For more information, or some great examples to practice with, check out this post at mathisfun.com. Also, the Wolfram Alpha page for cosine is also very helpful.
As I’ target=”_blank”m sure you’ve figured out already, my next post will be on the third of the three basic trig functions. (The suspense must be killing you!)