Triangle problems are some of the most common types of mathematics problems you will find when first studying geometry and trigonometry. Some might argue that one triangle concept in particular, the Pythagorean Theorem, is one of the most famous and well-known concepts of all! I have gone into detail on this blog about several trigonometry functions that are useful to help solve triangles, but in this post, I am going to talk about the geometric side. In particular, I’m going to show you how to calculate the area of a triangle. There are actually several ways of doing this. This should probably come as no surprise to you, though. There always seems to be more than one way to do things in math!
Probably the easiest way to do this requires that you know only two things about your triangle: the length of its base, and its height. With those numbers, you simply insert them into this equation and solve for the area:
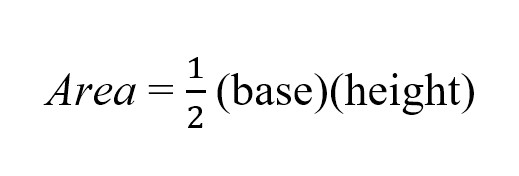
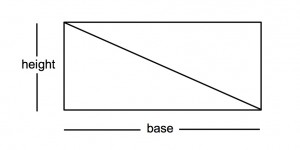
Pretty easy, right? Do you understand why this equation works, though? Take a look at the equation again. You might recognize that it looks familiar, almost like the equation to solve the area of a rectangle – only this time, multiply by a half. So the area of a triangle is equal to half of the area of a rectangle. You can very easily see this simply by drawing any old rectangle, label the sides as “base” and “height”, and then go ahead and draw in a diagonal line that connects two of the corners. You’ve just created two equal triangles, and each triangle is half of the original rectangle! Well, that’s great if you have a triangle that has one side perfectly horizontal, and the other 90 degrees up perfectly vertical. That is literally half of a rectangle. But what about triangles that have more irregular angles?
Like a triangle with 31, 82, and 67 degrees? No right angles there, and it certainly doesn’t look like half of a rectangle. Check this out though. It still works! Orient your triangle so that it’s long side is on the bottom. Then, draw in a line from its highest point straight down to intersect the bottom.
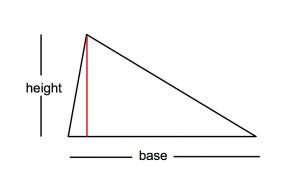
So far, we have just identified its base and its height. Now, for the fun part! Separate your triangle on the vertical line you just drew, and then take your two new smaller triangles and switch sides – put the one on the left over on the right now, but right next to each other, touching at their corner. Now we have a weird structure that has the same base length, and has two vertical walls that have the same height. Now if you just draw in another line to connect the two tops, you can create a rectangle. And, if you were to measure the area of the new triangle created when you connected the tops, you would find that its area is exactly equal to the area of your first triangle, and obviously together they form the complete area of the rectangle.
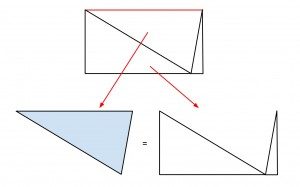
So, there you have it. Visual proof of the triangle area formula! That’s a fantastic method to use to find the area of the triangle if you know its base and height (or “altitude” as some may call it). But what about if you don’t know its height? The height of right angle triangles is easy because it is equal to one of the sides. But for other triangles, if you know the side lengths, that doesn’t always mean you can immediately determine the height. In that case, there is another formula that you can use, called Heron’s (or Hero’s) formula. You can use Heron’s formula to calculate the area of a triangle where you know the lengths of all of the sides.
Heron’s formula is sometimes referred to as the “irregular triangle calculation method,” and is named after Heron (or Hero) of Alexandria. Heron was an engineer and mathematician in Ancient Greece, who is credited with inventing many thing, including an early steam engine , a windwheel, and a vending machine. (Check out this Wikipedia page for more information on some of his inventions and accomplishments!) His formula for calculating the area of a triangle contains a few steps, but thankfully, they are not all that difficult. The first thing you have to do is to calculate the half-perimeter (or the semi-perimeter, s). You do this by simply summing the three side lengths (a, b, and c) and dividing in half. Once you’ve done that, then you just plug numbers into the following equation:
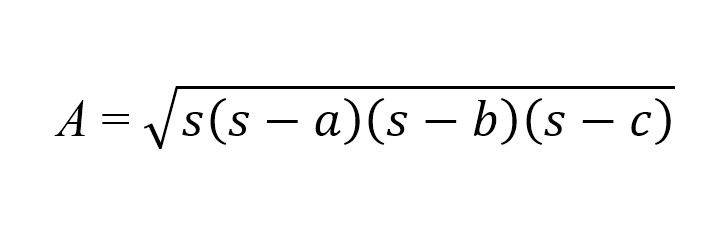
It might be easier to remember this equation by breaking it down and looking at what each part is. If you consider that the three bracketed terms are really just the difference in side length from the half-perimeter, then all you need to remember is to multiply those three values by the half-perimeter itself, and then square root the whole thing. I know that sounds like a mouthful, but having some degree of understanding about what more complex formulas are based on is always helpful.
Somewhat related to this method is a much simplified version, which is specifically applicable to equilateral triangles. (Of course, we all know that equilateral triangles are special triangles whose sides are equal and all angles are 60 degrees.) It’s a much simpler equation to remember, without needing to make a first calculation like with Heron’s formula. Here is the formula for the area of an equilateral triangle:
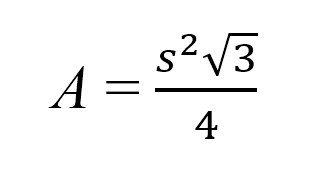
The final method that I will describe here uses trigonometry to find the area. You can use this formula on any triangle, provided that you know the length of two of the sides and the angle between them. (Note: there are variations of this formula, depending on what sides and angle are known). It’s fairly easy to remember, as long as you just think about ABC! Here’s the formula:
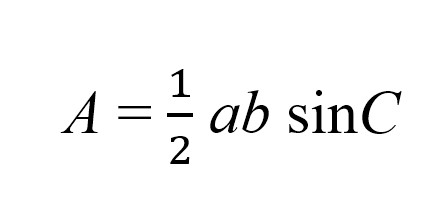
This goes back to my diagram above, with the inscribed “height” line in the triangle. Using a basic trig identity for sine, you can calculate the height using the hypotenuse of one of the smaller triangles and a known angle. Then, you simply take this trig formula and substitute it in for the height term in our original triangle area formula (1/2 base x height). With some simple rearranging, you can come up with our final half absinc formula here!
That’s all the methods that I’m going to discuss here, though you now know four ways of calculating the area of a triangle! Just pick the right methods for your specific problem, and you will only be a few steps away from solving the area!

