EDUCATION
Horizontal Translation: How to Shift Graphs
Shifting graphs horizontally (also known as horizontal translation) is slightly different from vertical translation, but still pretty straight-forward. Perhaps it would be helpful to review my posting on vertical shifts of graphs. Recall from that section: “Picture all the complex stuff that is happening to x as being one chunk of the height component, and then when you add the + 5 to the equation, you are really just adding an additional height chunk to the total height for a given x.” I think this simplification condenses the rest of that post down quite nicely.
Shifting Graphs – Horizontal Translation
Now, to shift a graph horizontally, you include the shift amount with x. So, whatever action was being done just to x before, now you do that same thing to x plus the shift amount. Make sense? Probably not.
Check out the example below that hopefully demonstrates this better than I can explain with words.
If you want to shift the original function of f(x) = x2 + 4 by 3 units, it becomes f(x) = (x-3)2 + 4.
Can you see what I mean by including the shift amount WITH x. The ‘square’ function acts on the entire (x-3) term. This will cause the graph to shift 3 units to the RIGHT. This may seem somewhat counter-intuitive, but it is correct. Subtracting terms from x shift the graph to the right, whereas adding terms to x will translate them to the left.
In this example, x-3 causes a horizontal translation of the graph 3 units right… if it were x+3, it would translate the graph 3 units left. Here is a bit of a trick you can use to help you recall the direction of the shift caused by the signs. It may be easier to remember this by analyzing the “x and shift amount”, letting this small term equal to 0, and then solving for x. The result will show you how many units to move, and in what direction. Like this:
x – 3 = 0
x = 3 (shift 3 units right)
OR
x + 3 = 0
x = (-3) (shift 3 units left)
That shows you how far over, and in what direction, the new x values are! Technically, this is a way of finding a zero of the graph, but that is another post for another day. For now, I think it’s a helpful trick to apply at this stage!
I hope these postings on graph manipulations are helpful. Horizontal translation of functions and their graphs is still quite simple, albeit with the trick with the signs that you don’t have to worry about with vertical translation.
ALSO READ: Using the Quadratic Formula
EDUCATION
Trigonometry: Special Angle Triangles

Trigonometry is the type of math that you use when you want to work with angles. Luckily, some angles are used so frequently that they have their own dedicated name and shortcuts that you can memorize. These are called special angles in trigonometry, and you can use special angle triangles to help.
Special angles are great to know because their trigonometric functions equate to very specific and known ratios, so if you can memorize these it will save you a lot of time in doing trigonometry homework! To make things a bit easier, if you can’t remember these exact values, it is even easier to memorize the special angle triangles that these angles are based off of! And there are only two triangles, so you will find that it is very easy to derive the trig functions if you can’t remember them.
Specifically, the trig functions are easy to find for these special angles, which are: 0, 30, 45, 60, and 90 degrees.
45-45-90 Triangle
This will hopefully make sense after looking at the triangles I mentioned. Here’s another site that also talks about remembering the patterns of these triangles instead of specifically remembering the math. Create a right angle triangle with two 45 degree angles, and with two sides of 1 unit length. By using the Theorem of Pythagoras, you can find that the hypotenuse of this triangle is easy to calculate to be length √2. This is what this triangle looks like:
So then, from these values and using the memorization trick of SOHCAHTOA (here a quick trig cheat sheet for reference), you can obtain the trigonometric values for this special angle of 45 degrees. You can work out that:
Sin(45) = 1/√2
Cos(45) = 1/√2
Tan(45) = 1
Don’t worry if you can’t remember these values and ratios. The easiest way to remember them is to memorize how to construct the special angle triangle. And as you can see, this triangle is very simple: a right angle triangle with a 45 degree angle and 2 sides of length 1, and you can easily fill in the rest and then work out the ratios yourself.
30-60-90 Triangle
The second of the special angle triangles, which describes the remainder of the special angles, is slightly more complex, but not by much. Create a right angle triangle with angles of 30, 60, and 90 degrees. The lengths of the sides of this triangle are 1, 2, √3 (with 2 being the longest side, the hypotenuse. Make sure you don’t put the √3 as the hypotenuse!). FreeMathHelp also has a good explanation of this particular triangle. This triangle looks like this:
Here are the trig ratios that you can easily find:
Sin(30) = 1/2
Cos(30) = √3/2
Tan(30) = 1/√3
Sin(60) = √3/2
Cos(60) = 1/2
Tan(60) = √3/1 = √3
Once again, just remember the triangle, and the ratios are easy to derive!
For 0 and 90 degrees, there isn’t a triangle to remember (although please feel free to correct me if I am wrong!), so you will actually have to memorize these values. However, these aren’t complex. I usually just remember the pattern of the following list:
Sin(0) = 0
Cos(0) = 1
Tan(0) = 0
Sin(90) = 1
Cos(90) = 0
Tan(90) = undefined
If you can’t memorize the actual trigonometric ratios for the special angles, the key is to recall the special angle triangles that describe them. Make sure that you know how to construct the triangles, and then you can solve the trig ratios of the trigonometry special angles. You will quickly find that doing trigonometry questions that use these special angles are easy!
(This is an old post from my previous math site, In Mathematics, copied here to consolidate all my math pages.)
EDUCATION
Logarithm Rules

In my previous post, I introduced the concept of logarithms to you. I explained how logarithms and exponents are connected, and then showed you a quick trick to help you remember how to convert between the two. Now in this post, I’m going to go a little bit deeper and explain a few rules of logarithms to help you actually do math with them. Considering how you now already know that logs and exponents are related, it should come as no surprise that, just like there is a set of exponent rules, there is also a set of logarithmic rules.
As you look at these logarithm rules, keep in mind that by convention, if you write logs without the subscript number to indicate their base, it is assumed that you are dealing in base–10. For simplicity, this is the convention that I am going to use in this post, though these rules certainly apply when dealing with logs of other bases.
With that intro out of the way, let’s get to it.

The first law of logarithms is the product rule. If you are familiar with the product rule of exponents, then this logarithm law should be a piece of cake for you. Where the exponent rule says that when multiplying exponential expressions with the same base, you simply add the exponents, this same thing applies when multiplying logarithms of the same base. Therefore, the rule states that the logarithm of a product is equal to the sum of the logarithms.
This rule is very commonly used, and it is important to recognize that you can use it in either direction. That is, the logarithm of a product converts to a sum of logarithms, and vice versa.

The next logarithmic law is the quotient rule. Again, this law can easily be derived by applying your knowledge of the exponent quotient rule (though I will leave that for you as an exercise). However, it does appear to look different. This rule states that the logarithm of a quotient is equal to the logarithm of the numerator minus the logarithm of the denominator. Sounds like a mouthful, but the expression is probably much simpler to understand.
Again, watch for opportunities to use this relationship in either direction!

The third law of logs is the power rule. This one is surprisingly simple to remember, and again can be found by manipulating exponent and logarithm laws. Quite simply, this law says that when you have a logarithm of an exponential expression, the exponent can be “brought out” of the log and used as a coefficient for the log.

The last of the rules of logarithms that I’m going to discuss here today is called the base change rule. Recall that I stated above that all of my examples that I’ve used so far in this post use the convention of an assumed base–10. If I wanted to change my expression to utilize a different base, this rule helps us to do that. So then, if I have my log in some base of a number, and I want to express this in terms of a different base, I simply take the log in my new base of the original number and divide that by the log in my new base of the original base. Sounds wordy, but again, a picture is worth a thousand words:
Here, my original base is B, and my new base that I want to express things in is X.
That is all I have to say about the rules of logarithms in this short introduction to them. They are fairly straight forward themselves, though can be used in very complex equations. I will try to do a separate post soon outlining some examples of all of these rules, though I do think that the general forms that I’ve noted above are pretty self-explanatory.
If you are interested in learning more about logarithms, there is a much more thorough summary of logarithms at the Learning and Teaching Math blog, which I highly recommend (for this and other math topics!)
EDUCATION
Pythagorean Identities
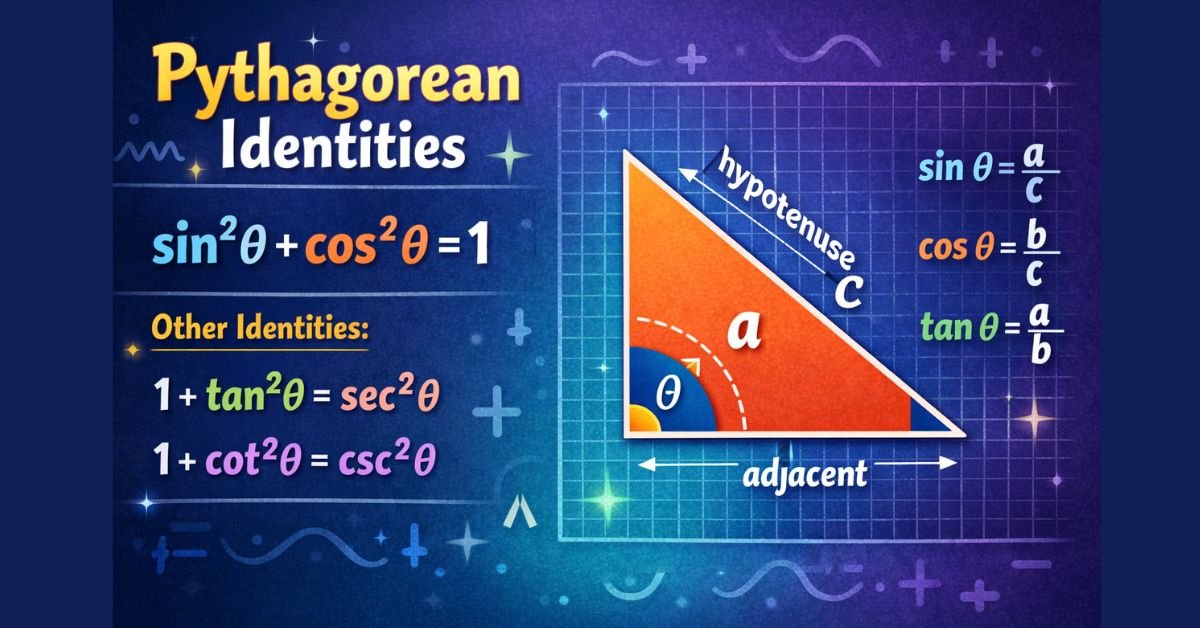
Pythagorean Identities in trigonometry will show up very frequently and can be very useful. I will explain how Pythagorean Identities get their name, how you can derive them, and how you can remember them. First, it would be a good idea for you to be able to understand the basic trig functions sine, cosine, and tangent. Once you are familiar with these trig equations, the algebra that we will apply to them will allow us to derive the Pythagorean Identities. I have prepared other posts on this site that are dedicated to sine, cosine, and tangent that may be useful to review.
The Pythagorean Identities get their name because they are based on the famous Theorem of Pythagoras. You are very likely already familiar with it. (On a side note, here are some interesting facts about the Theorem of Pythagoras.) Simply, for a right angle triangle, it says “the square of the hypotenuse is the sum of the squares of the other two sides.” Mathematically, you have seen this represented as:
a2 + b2 = c2, where a and b are sides and c is the hypotenuse.
Now, I will show you how to derive these special trig identities, using this theorem as our starting point. To do this, we need to start with a right triangle, created by the radius of a unit circle and the axis:
We can say that the right triangle formed by dropping a line from the point that the radius touches the circle (anywhere in quadrant I is sufficient for this demonstration) down to the axis has a base of x units long and y units high. (The actual numbers are not important, but they will depend on the specific angle, if you did need to calculate them for whatever reason. You don’t here.) The radius in a unit circle, by definition, is 1. Now, let’s apply the definitions of sine and cosine to our triangle. Recall:
sin(ɵ) = opposite / hypotenuse = y / 1 = y
cos(ɵ) = adjacent / hypotenuse = x / 1 = x
So, now we can relabel our diagram by substituting in these basic trig identities.
With the triangle now correctly labeled for our derivation, we can apply the Theorem of Pythagoras to arrive at one of the Pythagorean Identities. Since a2 + b2 = c2, we can therefore equate the sides of our triangle to these terms to give us our first of the trig Pythagorean Identities:
sin2(ɵ) + cos2(ɵ) = 1
If you have followed along up till now and understood everything I’ve done, then you are well on your way to remembering this trigonometric identity. If you can remember how to derive it, you don’t even have to memorize it (though it always helps!) For the next Pythagorean Identity, you start with this first identity, and you apply some basic algebra and trigonometry to it to derive the second and third identities. Recall the definitions of secant, cosecant, and cotangent:
sec(ɵ) = 1 / cos(ɵ)
csc(ɵ) = 1 / sin(ɵ)
cot(ɵ) = 1 / tan(ɵ) = cos(ɵ) / sin(ɵ)
With those inverse trig functions in mind, let’s take the first Pythagorean Identity and divide all of its terms by cos2(ɵ). That gives you:
1 / cos2(ɵ) = sin2(ɵ) / cos2(ɵ) + cos2(ɵ) / cos2(ɵ)
sec2(ɵ) = tan2(ɵ) + 1
And this is the second Pythagorean Identity! Using the same strategy we just used to derive that one, go back to the first one and divide everything by sin2(ɵ), to arrive at the third Pythagorean Identity!
csc2(ɵ) = 1 + cot2(ɵ)
I hope that from this tutorial, you now understand how these identities get their name, how you can derive them, and how to use this knowledge to help you to memorize or recall them. Using the fundamental trigonometry identities and trig relations, it is easy to come up with more advanced trigonometric formulas. If you need to refer back to this Pythagorean Identities list, please bookmark this page and come back again. Also, be sure to follow me on Facebook/Twitter/Google+ (@TheNumerist). Thanks.
(This is an old post from my previous math site, In Mathematics, copied here to consolidate all my math pages.)
-

 TECH6 months ago
TECH6 months agoApple iPhone 17: Official 2025 Release Date Revealed
-

 BLOG6 months ago
BLOG6 months agoUnderstanding the ∴ Symbol in Math
-

 EDUCATION6 months ago
EDUCATION6 months agoUsing the Quadratic Formula
-

 EDUCATION6 months ago
EDUCATION6 months agoThe Meaning of an Open Circle in Math Explained
-

 HEALTH6 months ago
HEALTH6 months agoGoodNever: Wellness, Simplified
-

 EDUCATION6 months ago
EDUCATION6 months agoWhy Does m Represent Slope?
-

 EDUCATION6 months ago
EDUCATION6 months agoHow to Solve Quadratic Equations 2
-

 ENTERTAINMENT6 months ago
ENTERTAINMENT6 months agoGoing Live: How to Stream on TikTok from Your PC
