EDUCATION
Inside GIPS: Fresh Stories from Grand Island Public Schools

Grand Island Public Schools (GIPS) continues to be a dynamic educational district in Nebraska, setting benchmarks in innovation, community involvement, and student achievement. As families, educators, and stakeholders keep a close eye on the evolving academic landscape, GIPS remains committed to shaping the future of learning by fostering inclusive practices, modern curriculum approaches, and student-first policies. These fresh stories from the district offer a closer look at how Grand Island is building a stronger educational foundation through community-driven initiatives, progressive leadership, and student empowerment.
Empowering Students Through Academic Innovation
At the heart of GIPS’s mission is a dedication to academic excellence. The district has embraced project-based learning, personalized education plans, and digital literacy integration to equip students for college, careers, and beyond. With the use of technology-enhanced classrooms and 1:1 Chromebook programs, students are gaining access to real-time resources that allow them to develop critical thinking and digital citizenship skills.
Additionally, curriculum enhancements in STEM (Science, Technology, Engineering, and Mathematics) programs are opening doors for middle and high school students. By encouraging hands-on experimentation and coding in elementary grades, the district aims to build a pipeline of future innovators and engineers.

Diversity, Equity, and Inclusion in Education
Grand Island Public Schools prides itself on serving a diverse student population that reflects the changing demographics of the United States. With over 40 languages spoken among students and families, the district’s multilingual programs, including Dual Language Immersion and English Language Learner (ELL) support, have become essential to student success.
Equity-focused strategies have been embedded into GIPS policies to ensure fair access to education regardless of a student’s background. The district’s cultural liaisons and community engagement specialists work to close achievement gaps, offering tailored support for underrepresented groups and students with special needs. These initiatives align with national priorities for equity in K-12 education and are shaping a more inclusive academic environment.
Teacher Development and Leadership Training
Recognizing that empowered educators lead to empowered students, GIPS has invested significantly in professional development. Teachers across all grade levels participate in ongoing training sessions centered on trauma-informed teaching, social-emotional learning (SEL), and differentiated instruction.
Furthermore, the district has launched leadership academies to groom future principals and instructional coaches from within its ranks. By nurturing talent internally, GIPS maintains continuity in its educational philosophy and strengthens leadership capacity at the school level.
In collaboration with local universities and teacher preparation programs, the district also hosts student-teacher residencies, bridging the gap between theory and practice. This fosters a pipeline of passionate, well-prepared educators ready to meet the unique challenges of 21st-century classrooms.
Extracurriculars and Student Voice
Beyond academics, Grand Island Public Schools has made student engagement a top priority. From award-winning debate teams to thriving arts and theater programs, students have ample opportunities to find their passions and express their creativity.
Athletics remain a cornerstone of school spirit and character-building. GIPS encourages participation in sports not only for physical fitness but also to foster teamwork, perseverance, and discipline. The district’s emphasis on Title IX compliance ensures equal opportunities for all students, regardless of gender or ability.
Student councils and advisory boards across schools give young voices a platform to influence decision-making processes. Whether it’s planning events, promoting anti-bullying campaigns, or suggesting cafeteria menu changes, students play a direct role in shaping their school culture.

Parent Engagement and Community Partnerships
The success of GIPS is strongly tied to the support and collaboration of families and local organizations. Parent-teacher associations (PTAs), booster clubs, and family resource centers provide avenues for parental involvement and two-way communication.
GIPS has also partnered with local businesses and nonprofits to expand opportunities for students, particularly in career and technical education (CTE). Internships, job shadowing, and mentorship programs expose high schoolers to potential career paths and equip them with real-world experience.
Additionally, community health partnerships ensure students have access to mental health services, dental screenings, and nutrition support—demonstrating GIPS’s commitment to the whole-child approach.
Facility Upgrades and Sustainability Goals
Modern learning requires modern spaces, and GIPS has embarked on major capital improvement projects to upgrade facilities across the district. These upgrades include secure entryways, advanced HVAC systems, and energy-efficient lighting.
Green initiatives such as school gardens, recycling programs, and solar energy pilot projects reflect the district’s broader sustainability goals. By involving students in environmental stewardship, GIPS is instilling responsibility and awareness from a young age.
The opening of new early childhood centers and career academies further exemplifies the district’s commitment to preparing students from cradle to career.
Responding to Challenges with Resilience
Like many public school districts, Grand Island Public Schools faced significant challenges during the COVID-19 pandemic. However, the district’s swift transition to remote learning and later, hybrid models, highlighted its adaptability and technological readiness.
GIPS also expanded meal distribution programs, mental health services, and Wi-Fi hotspots to support families during uncertain times. The district’s crisis response plan now serves as a blueprint for resilience and continuity in the face of future disruptions.
With a renewed focus on student attendance, mental health, and learning recovery, GIPS continues to evolve and adapt to ensure no child is left behind.
Looking Ahead: Strategic Goals for the Future
GIPS is not just reacting to present needs—it is planning proactively for the future. The district’s five-year strategic plan emphasizes student-centered learning, equity, family engagement, and operational efficiency.
Future goals include expanding dual-credit college courses, increasing high school graduation rates, and enhancing special education programming. GIPS is also exploring AI-driven personalized learning tools to tailor instruction and assessments based on individual learning styles and progress.
Community input continues to shape the district’s priorities, with school board meetings and town halls serving as key forums for collaboration.
Frequently Asked Questions (FAQs)
Q1: What makes Grand Island Public Schools different from other districts in Nebraska?
GIPS stands out for its diversity, equity-focused programs, strong community partnerships, and innovative curriculum that includes personalized learning and robust STEM education.
Q2: How does GIPS support English Language Learners?
The district offers tailored support such as Dual Language Immersion programs, ESL instruction, and cultural liaison services to ensure language is not a barrier to academic success.
Q3: Are there opportunities for students to gain real-world experience?
Yes, GIPS partners with local businesses to provide internships, job shadowing, and career mentoring through its Career Pathways and CTE programs.
Q4: How can parents get involved in GIPS schools?
Parents can participate in PTAs, attend school board meetings, volunteer in classrooms, and engage through digital platforms like parent portals and newsletters.
Q5: What kind of support is available for students’ mental health?
GIPS offers counseling services, peer support programs, and collaborates with health organizations to provide accessible mental health resources for students and families.
Conclusion
Inside GIPS: Fresh Stories from Grand Island Public Schools highlights a district that is deeply committed to nurturing every student’s potential through innovation, inclusivity, and partnership. As Grand Island continues to evolve in response to educational trends and community needs, its schools remain a vital part of the city’s heartbeat—where the future is being built one student at a time. Whether through academic growth, cultural celebration, or future-focused planning, GIPS exemplifies what it means to be a forward-thinking public school system.
EDUCATION
Trigonometry: Special Angle Triangles

Trigonometry is the type of math that you use when you want to work with angles. Luckily, some angles are used so frequently that they have their own dedicated name and shortcuts that you can memorize. These are called special angles in trigonometry, and you can use special angle triangles to help.
Special angles are great to know because their trigonometric functions equate to very specific and known ratios, so if you can memorize these it will save you a lot of time in doing trigonometry homework! To make things a bit easier, if you can’t remember these exact values, it is even easier to memorize the special angle triangles that these angles are based off of! And there are only two triangles, so you will find that it is very easy to derive the trig functions if you can’t remember them.
Specifically, the trig functions are easy to find for these special angles, which are: 0, 30, 45, 60, and 90 degrees.
45-45-90 Triangle
This will hopefully make sense after looking at the triangles I mentioned. Here’s another site that also talks about remembering the patterns of these triangles instead of specifically remembering the math. Create a right angle triangle with two 45 degree angles, and with two sides of 1 unit length. By using the Theorem of Pythagoras, you can find that the hypotenuse of this triangle is easy to calculate to be length √2. This is what this triangle looks like:
So then, from these values and using the memorization trick of SOHCAHTOA (here a quick trig cheat sheet for reference), you can obtain the trigonometric values for this special angle of 45 degrees. You can work out that:
Sin(45) = 1/√2
Cos(45) = 1/√2
Tan(45) = 1
Don’t worry if you can’t remember these values and ratios. The easiest way to remember them is to memorize how to construct the special angle triangle. And as you can see, this triangle is very simple: a right angle triangle with a 45 degree angle and 2 sides of length 1, and you can easily fill in the rest and then work out the ratios yourself.
30-60-90 Triangle
The second of the special angle triangles, which describes the remainder of the special angles, is slightly more complex, but not by much. Create a right angle triangle with angles of 30, 60, and 90 degrees. The lengths of the sides of this triangle are 1, 2, √3 (with 2 being the longest side, the hypotenuse. Make sure you don’t put the √3 as the hypotenuse!). FreeMathHelp also has a good explanation of this particular triangle. This triangle looks like this:
Here are the trig ratios that you can easily find:
Sin(30) = 1/2
Cos(30) = √3/2
Tan(30) = 1/√3
Sin(60) = √3/2
Cos(60) = 1/2
Tan(60) = √3/1 = √3
Once again, just remember the triangle, and the ratios are easy to derive!
For 0 and 90 degrees, there isn’t a triangle to remember (although please feel free to correct me if I am wrong!), so you will actually have to memorize these values. However, these aren’t complex. I usually just remember the pattern of the following list:
Sin(0) = 0
Cos(0) = 1
Tan(0) = 0
Sin(90) = 1
Cos(90) = 0
Tan(90) = undefined
If you can’t memorize the actual trigonometric ratios for the special angles, the key is to recall the special angle triangles that describe them. Make sure that you know how to construct the triangles, and then you can solve the trig ratios of the trigonometry special angles. You will quickly find that doing trigonometry questions that use these special angles are easy!
(This is an old post from my previous math site, In Mathematics, copied here to consolidate all my math pages.)
EDUCATION
Logarithm Rules

In my previous post, I introduced the concept of logarithms to you. I explained how logarithms and exponents are connected, and then showed you a quick trick to help you remember how to convert between the two. Now in this post, I’m going to go a little bit deeper and explain a few rules of logarithms to help you actually do math with them. Considering how you now already know that logs and exponents are related, it should come as no surprise that, just like there is a set of exponent rules, there is also a set of logarithmic rules.
As you look at these logarithm rules, keep in mind that by convention, if you write logs without the subscript number to indicate their base, it is assumed that you are dealing in base–10. For simplicity, this is the convention that I am going to use in this post, though these rules certainly apply when dealing with logs of other bases.
With that intro out of the way, let’s get to it.

The first law of logarithms is the product rule. If you are familiar with the product rule of exponents, then this logarithm law should be a piece of cake for you. Where the exponent rule says that when multiplying exponential expressions with the same base, you simply add the exponents, this same thing applies when multiplying logarithms of the same base. Therefore, the rule states that the logarithm of a product is equal to the sum of the logarithms.
This rule is very commonly used, and it is important to recognize that you can use it in either direction. That is, the logarithm of a product converts to a sum of logarithms, and vice versa.

The next logarithmic law is the quotient rule. Again, this law can easily be derived by applying your knowledge of the exponent quotient rule (though I will leave that for you as an exercise). However, it does appear to look different. This rule states that the logarithm of a quotient is equal to the logarithm of the numerator minus the logarithm of the denominator. Sounds like a mouthful, but the expression is probably much simpler to understand.
Again, watch for opportunities to use this relationship in either direction!

The third law of logs is the power rule. This one is surprisingly simple to remember, and again can be found by manipulating exponent and logarithm laws. Quite simply, this law says that when you have a logarithm of an exponential expression, the exponent can be “brought out” of the log and used as a coefficient for the log.

The last of the rules of logarithms that I’m going to discuss here today is called the base change rule. Recall that I stated above that all of my examples that I’ve used so far in this post use the convention of an assumed base–10. If I wanted to change my expression to utilize a different base, this rule helps us to do that. So then, if I have my log in some base of a number, and I want to express this in terms of a different base, I simply take the log in my new base of the original number and divide that by the log in my new base of the original base. Sounds wordy, but again, a picture is worth a thousand words:
Here, my original base is B, and my new base that I want to express things in is X.
That is all I have to say about the rules of logarithms in this short introduction to them. They are fairly straight forward themselves, though can be used in very complex equations. I will try to do a separate post soon outlining some examples of all of these rules, though I do think that the general forms that I’ve noted above are pretty self-explanatory.
If you are interested in learning more about logarithms, there is a much more thorough summary of logarithms at the Learning and Teaching Math blog, which I highly recommend (for this and other math topics!)
EDUCATION
Pythagorean Identities
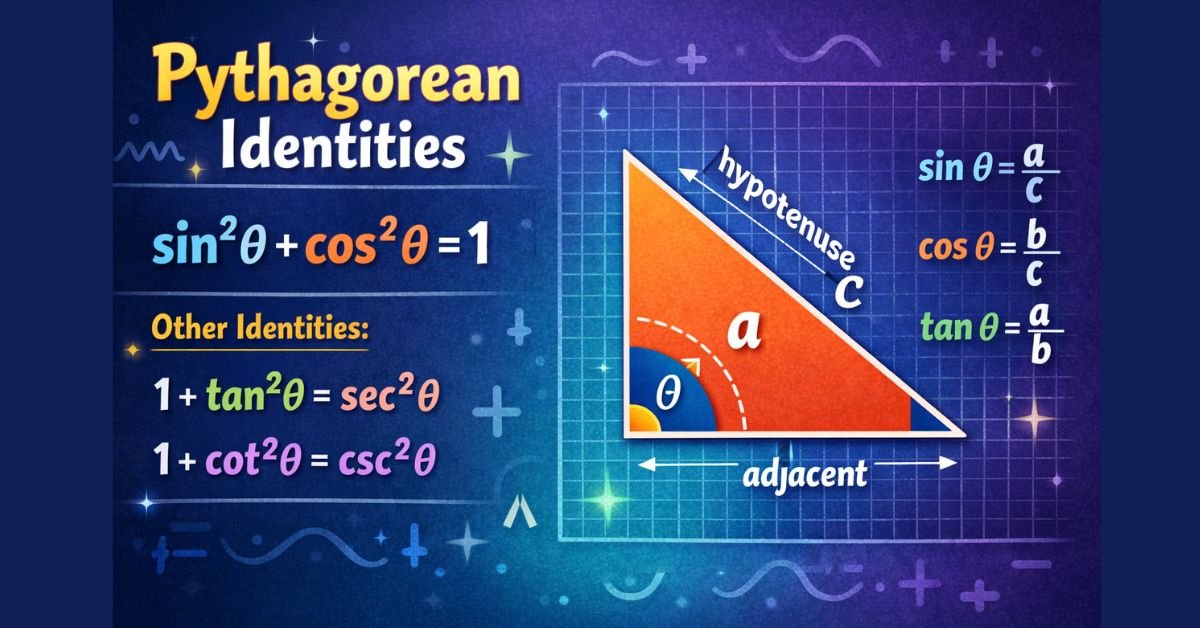
Pythagorean Identities in trigonometry will show up very frequently and can be very useful. I will explain how Pythagorean Identities get their name, how you can derive them, and how you can remember them. First, it would be a good idea for you to be able to understand the basic trig functions sine, cosine, and tangent. Once you are familiar with these trig equations, the algebra that we will apply to them will allow us to derive the Pythagorean Identities. I have prepared other posts on this site that are dedicated to sine, cosine, and tangent that may be useful to review.
The Pythagorean Identities get their name because they are based on the famous Theorem of Pythagoras. You are very likely already familiar with it. (On a side note, here are some interesting facts about the Theorem of Pythagoras.) Simply, for a right angle triangle, it says “the square of the hypotenuse is the sum of the squares of the other two sides.” Mathematically, you have seen this represented as:
a2 + b2 = c2, where a and b are sides and c is the hypotenuse.
Now, I will show you how to derive these special trig identities, using this theorem as our starting point. To do this, we need to start with a right triangle, created by the radius of a unit circle and the axis:
We can say that the right triangle formed by dropping a line from the point that the radius touches the circle (anywhere in quadrant I is sufficient for this demonstration) down to the axis has a base of x units long and y units high. (The actual numbers are not important, but they will depend on the specific angle, if you did need to calculate them for whatever reason. You don’t here.) The radius in a unit circle, by definition, is 1. Now, let’s apply the definitions of sine and cosine to our triangle. Recall:
sin(ɵ) = opposite / hypotenuse = y / 1 = y
cos(ɵ) = adjacent / hypotenuse = x / 1 = x
So, now we can relabel our diagram by substituting in these basic trig identities.
With the triangle now correctly labeled for our derivation, we can apply the Theorem of Pythagoras to arrive at one of the Pythagorean Identities. Since a2 + b2 = c2, we can therefore equate the sides of our triangle to these terms to give us our first of the trig Pythagorean Identities:
sin2(ɵ) + cos2(ɵ) = 1
If you have followed along up till now and understood everything I’ve done, then you are well on your way to remembering this trigonometric identity. If you can remember how to derive it, you don’t even have to memorize it (though it always helps!) For the next Pythagorean Identity, you start with this first identity, and you apply some basic algebra and trigonometry to it to derive the second and third identities. Recall the definitions of secant, cosecant, and cotangent:
sec(ɵ) = 1 / cos(ɵ)
csc(ɵ) = 1 / sin(ɵ)
cot(ɵ) = 1 / tan(ɵ) = cos(ɵ) / sin(ɵ)
With those inverse trig functions in mind, let’s take the first Pythagorean Identity and divide all of its terms by cos2(ɵ). That gives you:
1 / cos2(ɵ) = sin2(ɵ) / cos2(ɵ) + cos2(ɵ) / cos2(ɵ)
sec2(ɵ) = tan2(ɵ) + 1
And this is the second Pythagorean Identity! Using the same strategy we just used to derive that one, go back to the first one and divide everything by sin2(ɵ), to arrive at the third Pythagorean Identity!
csc2(ɵ) = 1 + cot2(ɵ)
I hope that from this tutorial, you now understand how these identities get their name, how you can derive them, and how to use this knowledge to help you to memorize or recall them. Using the fundamental trigonometry identities and trig relations, it is easy to come up with more advanced trigonometric formulas. If you need to refer back to this Pythagorean Identities list, please bookmark this page and come back again. Also, be sure to follow me on Facebook/Twitter/Google+ (@TheNumerist). Thanks.
(This is an old post from my previous math site, In Mathematics, copied here to consolidate all my math pages.)
-

 TECH6 months ago
TECH6 months agoApple iPhone 17: Official 2025 Release Date Revealed
-

 BLOG6 months ago
BLOG6 months agoUnderstanding the ∴ Symbol in Math
-
 EDUCATION6 months ago
EDUCATION6 months agoHorizontal Translation: How to Shift Graphs
-

 EDUCATION6 months ago
EDUCATION6 months agoUsing the Quadratic Formula
-

 EDUCATION6 months ago
EDUCATION6 months agoThe Meaning of an Open Circle in Math Explained
-

 HEALTH6 months ago
HEALTH6 months agoGoodNever: Wellness, Simplified
-

 EDUCATION6 months ago
EDUCATION6 months agoWhy Does m Represent Slope?
-

 EDUCATION6 months ago
EDUCATION6 months agoHow to Solve Quadratic Equations 2
